Квазипериодический режим
Cтраница 2
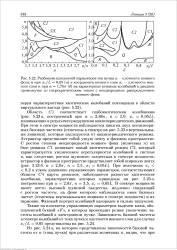
Арнольда, а множество точек, где показатель нулевой, - множеству сохранившихся на критической линии квазипериодических режимов. В нижней части рисунка представлены диаграммы, показывающие детали структуры в окрестности точки г гс, так что каждая последующая представляет собой увеличенный фрагмент предыдущей. [17]
Области периодичности имеют вид языков, подходящих сверху к линии J 1, а в промежутках между языками реализуются квазипериодические режимы. Бифуркация рождения тора из предельного цикла носит название бифуркации Неймарка. Дальнейшая эволюция аттрактора при изменении управляющего параметра может быть разнообразной и сложной, но в общем можно сказать, что реализуется та ситуация, о которой говорят как о переходе к хаосу через квазипериодичность. [18]
При k О число вращения w А / 2тг, так что при рациональных значениях А / 2тг имеют место периодические, а при иррациональных - квазипериодические режимы. На плоскости параметров области периодичности имеют вид характерных языков ( языки Арнольда), которые остриями подходят к рациональным точкам оси абсцисс. [19]
 |
Перемежающаяся турбулентность в гидродинамическом течении. [20] |
Итак, в итоге изучения вопроса о переходе динамических систем к хаосу сложилось представление о трех основных сценариях, а именно: через каскад удвоений периода, перемежаемость и квазипериодические режимы. Оставшаяся часть нашего курса будет посвящена рассмотрению этих сценариев и, соответствующих им особенностей сложной динамики нелинейных систем в области перехода от порядка к хаосу. [21]
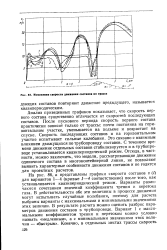 |
Изменение скорости движения составов по трассе. [22] |
На рис. 86, а представлены графики скорости составов и ( /) для вариантов 1 - 4 ( кривые 1 - 4 соответственно) после того, как устанавливается квазипериодический режим. Варианты различаются сочетанием значений коэффициента трения и перетока газа. В действительности обе эти величины в процессе движения могут испытывать случайные колебания, поэтому для расчета выбраны варианты с максимальными и минимальными значениями этих величин. [23]
При общем обсуждении проблемы перехода к хаосу мы говорили, что в многомерных нелинейных системах хаосу часто предшествует несколько бифуркаций рождения колебательных составляющих, отношение частот которых, вообще говоря, зависит от параметров задачи. Когда оно иррационально, реализуются квазипериодические режимы. В фазовом пространстве им соответствуют аттракторы в виде торов, размерность которых определяется количеством основных частотных компонент. При отношениях частот близких к рациональным из-за присущей системе нелинейности эти компоненты взаимодействуют, обнаруживая тенденцию к взаимной синхронизации ( захвату частот, mode locking) с возникновением периодических режимов. Квазипериодические и периодические режимы в свою очередь могут претерпевать различные бифуркации. [24]
Таким образом в эксперименте добивались квазипериодического режима: 4-часовая расстройка слишком велика и внутренний генератор не захватывается внешней силой. Анализируя такой сигнал с помощью специального спектрального метода, можно точно определить неизвестный период; он и интерпретируется как внутренний период генератора. Однако эта интерпретация сомнительна. Ниоткуда не следует, что эта разность должна быть мала. [25]
Это означает, что при каждом е имеется упорядоченная последовательность интервалов синхронизации со всеми возможными рациональными числами вращения. В частности, эти интервалы всюду плотны: между любыми двумя квазипериодическими режимами с различными числами вращения есть область синхронизации. [26]
На самом деле на рисунке видны только самые широкие языки, полное же число языков бесконечно - из каждой рациональной точки г на оси k 0 исходит острием свой язык. Пока параметр k невелик, между языками остается все же место для квазипериодических режимов. [28]
На двухмерной поверхности ( например, при намотке фазовой траектории на поверхность тора в трехмерном пространстве) странного аттрактора быть не может, так как нельзя избежать точек, в которых траектория пересекается сама с собой. Следовательно, появление странного аттрактора возможно не ранее чем на третьей бифуркации после разрушения двухчастотного квазипериодического режима и возникновения трехчастотного движения, фазовая траектория для которого будет располагаться на трехмерной поверхности тора в четырехмерном пространстве. [29]
Страницы: 1 2 3