Квазипериодический режим

Cтраница 3

Область ( 71 соответствует слабохаотическим колебаниям ( рис. 5.23 а, построенный при а 2 86тг, п 2 0, Х - 0 05L), возникающих в результате разрушения квазипериодических движений. При этом в спектре мощности наблюдаются пики на двух несоизмеримых базовых частотах ( отмечены в спектре на рис. 5.23 а вертикальными линиями), которые наследуются от квазипериодического режима. Аттрактор представляет собой узкую ленту в фазовом пространстве. В спектре мощности имеет место высокий шумовой пьедестал, медленно спадающий с ростом частоты, на фоне которого наблюдаются пики базовых частот ( отмечены вертикальными линиями в спектре мощности) и их гармоник. Фазовый портрет колебаний однороден и сильно зашумлен. [31]

С топологической точки зрения квазипериодические режимы неустойчивы, а синхронные устойчивы: при фиксированном е и изменении г синхронные режимы наблюдаются на интервалах ту, а квазипериодические - в отдельных точках. Это означает, что квазипериодическое движение можно разрушить сколь угодно малым возмущением. Однако с вероятностной точки зрения квазипериодические режимы преобладают 11 поскольку, как было доказано Арнольдом [1961], при малых е мера Лебега всех интервалов синхронизации стремится к нулю при е - 0; это означает, что возмущения, разрушающие квазипериодичность, довольно маловероятны. [32]

Еще более интересны и полны глубокой значимости результаты, получаемые при исследованиях химических реакций. В области, далекой от равновесия, оказывается возможным спонтанное возникновение упорядоченных структур с неоднородным, квазипериодическим распределением компонентов смеси в пространстве. Возможно также упорядочение процессов реакций во времени с возникновением периодических или квазипериодических режимов. И те, и другие случаи упорядочения обнаружены для различных реакций и в экспериментах. [33]

При k - - 0 суммарная длина всех ступенек чертовой лестницы стремится к нулю. При увеличении k она монотонно возрастает и при k 1 становится равной единице. Множество значений параметра А / 2тг, не принадлежащих ступенькам, соответствует иррациональным числам вращения и квазипериодическим режимам динамики. [34]

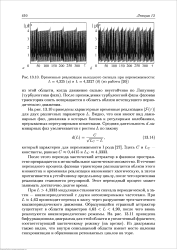Временные реализации выходного сигнала при перемежаемости. L 4 325 ( о и L 4 3327 ( б ( из работы. [35]

При L 4 3333 модуляция становится сначала периодической, а затем - квазипериодической с двумя несоизмеримыми частотами. При L РЙ 4 63 происходит переход к хаосу через разрушение трехчастотного квазипериодического движения. Образующийся странный аттрактор существует в области параметров 4 63 L 4 90, после чего вновь реализуются квазипериодические режимы. Из диаграммы также видно, что внутри описываемой области имеют место явления синхронизации и образования резонансных циклов на торе. [36]

В заключение отметим работу [38], посвященную анализу структуры бифуркационной диаграммы для динамических систем, содержащих седловое состояние равновесия, неустойчивое многообразие которого состоит из двух симметричных одномерных сепаратрис. Примером может служить система галеркинских уравнений, описывающая режимы тепловой конвекции в поле вибрации при слабом нарушении инверсионной симметрии. Рассмотрена ситуация, когда возникающие в системе го-моклинные петли являются притягивающими. В области регулярного поведения обнаружены, помимо периодических, квазипериодические режимы, которым соответствуют инвариантные множества канторотора Граница области хаоса оказывается фрактальной. [37]

Анализ приведенных графиков показывает, что скорость первого состава существенно отличается от скоростей последующих составов. После пускового периода скорость первого состава практически зависит только от трассы: почти постоянна на горизонтальном участке, уменьшается на подъеме и возрастает на спуске. Скорость последующих составов и на горизонтальном участке испытывает сильные колебания. Это связано с взаимным влиянием движущихся по трубопроводу составов. С течением времени движение отдельных составов стабилизируется и в трубопроводе устанавливается квазипериодический режим. Отсюда, в частности, можно заключить, что модели, рассматривающие движение одиночного состава в многоконтейнерной линии, не позволяют выявить характерные особенности движения составов и не годятся для проектных расчетов. [38]

Страницы: 1 2 3