Значение - подынтегральная функция
Cтраница 1
Значения подынтегральных функций этого уравнения м-огут быть заранее вычислены для различных значений температуры и сведены в таблицу. [1]
Если значения подынтегральной функции не могут быть найдены в этих точках из-за особенностей f ( x), то предположение, что подынтегральная функция может быть хорошо аппроксимирована многочленом, вероятно, неверно. [2]
Составим таблицу значений подынтегральной функции. [3]
Составляем таблицу значений подынтегральной функции у ех ( табл. 1.2), записывая ординаты с четными и с нечетными номерами в разные столбцы. В последней строке таблицы записываем результаты суммирования по этим столбцам. [4]
Составляем таблицу значений подынтегральной функции ( табл. 1.3), записывая эти значения в три столбца в зависимости от номера. [5]
Поскольку вычисление каждого значения подынтегральной функции требует обычно большого числа арифметических операций, уже при s 6 такое требование на число узлов оказывается практически невыполнимым. [6]
Так как изменение значений подынтегральных функций на множестве меры 0 не меняют значения интеграла, то мы можем считать, что gnm f g всюду. [7]
Чтобы повторно не вычислять значения подынтегральной функции во внутренних узлах на границах интервалов, на каждом из которых применяется формула Симпсона, соответствующие значения функции удваиваются после цикла Функции в узлах, совпадающих с пределами интегрирования, суммируются без удвоения. [8]
В табл. 68 приведены значения подынтегральных функций и интегралов для уравнения ( 6), из которого находится температура, уравнения ( 7), определяющего потерю напора, и уравнения ( 8), по которому рассчитываем объел реактора. [9]
В табл. 68 приведены значения подынтегральных функций и интегралов для уравнения ( 6), из которого находится температура, уравнения ( 7), определяющего потерю напора, и уравнения ( 8), по которому рассчитываем объем реактора. [10]
В табл. 68 приведены значения подынтегральных функций и интегралов для уравнения ( 6), из которого находится температура, уравнения ( 7), определяющего потерю напора, и уравнения ( 8), по которому рассчитываем объем реактора. [11]
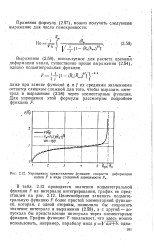 |
Упрощенное представление функции скорости деформации капли - F в виде степенной зависимости f. [12] |
В табл. 2.12 приводятся значения подынтегральной функции F на интервале интегрирования, график ее представлен на рис. 2.12. Целесообразно заменить подынтегральную функцию F более простой элементарной функцией, которая, с одной стороны, позволила бы сохранить значение интеграла в выражении (2.58), а с другой - допускала бы представление интеграла через элементарные функции. [13]
Суммирование указанных двух групп значений подынтегральной функции может быть выполнено в цикле. Во внешнем цикле вычисляется интеграл Q в интервале значений параметра Р от РО до РК. [14]
Суммирование указанных двух групп значений подынтегральной функции может быть выполнено в цикле. [15]
Страницы: 1 2 3 4