Конфокальный резонатор

Cтраница 2

Большой интерес представляет вычисление добротностей колебаний конфокального резонатора, что позволит определить возможности подавления высших типов колебаний. [16]

Пространственное амплитудно-фазовое распределение поля в случае конфокального резонатора образует характерный пучок - так называемый гауссов пучок. [17]

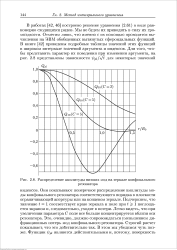Распределение амплитуды низших мод на зеркале конфокального. [18]

Они показывают поперечное распределение амплитуды моды конфокального резонатора соответствующего порядка в плоскости ограничивающей апертуры или на концевом зеркале. Подчеркнем, что значение t - 1 соответствует краю зеркала и поле при t 1 поглощается экраном и, следовательно, уходит в потери. Легко видеть, что при увеличении параметра С поле все больше концентрируется вблизи оси резонатора. Это, очевидно, должно сопровождаться уменьшением дифракционных потерь мод конфокального резонатора. Строгий расчет показывает, что это действительно так. [19]

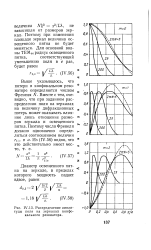Распределение ампли. [20]

Выше указывалось, что потери в конфокальном резонаторе определяются числом Френеля N. Вместе с тем, очевидно, что при заданном распределении поля на зеркалах на величину дифракционных потерь может оказывать влияние лишь отношение размеров зеркала и освещенного пятна. [21]

Открытый объемный резонатор. [22]

Общим для всех типов колебаний в конфокальном резонаторе является то, что поля этих типов колебаний локализованы в относительно узкой околоосевой области. [23]

В соответствии с выражением (7.16.8) в конфокальном резонаторе с зеркалами в виде двух бесконечных полос фазовый сдвиг / Зп [ см. соотношение (7.14.10) ] кратен тг / 2, так что в том же резонаторе с прямоугольными зеркалами фазовый сдвиг / 3 / т будет кратен тг / 2 / Заметим, что данное утверждение справедливо для любых резонаторов с конечным размером зеркал. [24]

Несимметричный двухзер. [25]

С этой целью следует выполнить вычисление для эквивалентного конфокального резонатора. [26]

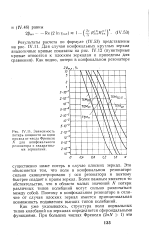Зависимость потерь мощности за один проход от числа Френеля Л для конфокального резонатора с квадратными зеркалами. [27]

Это объясняется тем, что поле в конфокальном резонаторе сильно сконцентрировано у оси резонатора и поэтому быстрее спадает к краям зеркал. Более важным является то обстоятельство, что в области малых значений N потери различных типов колебаний могут сильно различаться между собой. Поэтому в конфокальном резонаторе в отличие от случая плоских зеркал имеется принципиальная возможность подавления высших типов колебаний. [28]

Укажем лишь, что, например, для конфокального резонатора получатся те же результаты, которые уже были приведены в предыдущем разделе. [29]

На рис. 3.5 приведены значения коэффициентов потерь для цилиндрических конфокальных резонаторов. [30]

Страницы: 1 2 3 4