Конфокальный резонатор

Cтраница 3

Это соотношение позволяет найти расходимость излучения лазера с конфокальным резонатором, не детализируя модовый состав излучения, поскольку она справедлива, как для одномодового излучения, так и для излучения, состоящего из смеси поперечных мод, если предположить, что расходимость многомодового пучка определяется расходимостью моды максимального порядка. [31]

Смещение оптической оси, вызванное наклоном зеркала. [32]

Из этих выражений видно, что потери в конфокальных резонаторах сильнее зависят от модовых индексов / и р, чем в плоскопараллельных. В табл. 7.4 приводятся величины отношений api / aw потерь за один проход для плоского и конфокального резонаторов. Таким образом, становится понятным, почему по сравнению с другими резонаторами в плоскопараллельном резонаторе основная мода легче распадается на моды высоких порядков в результате рассеяния на неоднородностях среды ( например, на частицах пыли на зеркалах) и других препятствиях. [33]

Схема лазера с вогнутым сферическим и плоским зеркалами.| Схема лазера с двумя конфокальными сферическими зеркалами. [34]

Довольно часто применяется и другая схема, а именно конфокальный резонатор, в котором центр одного из зеркал совмещен с фокусом другого зеркала. Плоскопараллельные зеркала часто предусматривают на концевых поверхностях самого лазерного стержня. В других вариантах одно или оба зеркала устанавливаются вне активной среды лазера. [35]

R 2 102 см. Оказалось, что собственная мода конфокального резонатора не является собственным пучком оптической линии задержки, так как после ряда последовательных отражений она заметно расширяется. [36]

Заметим, что частотное вырождение, которое наблюдается для конфокального резонатора ( рис. 4.29), в обобщенном сферическом резонаторе снимается. [37]

Поэтому рассмотрение резонаторов других конфигураций часто сводят к поискам эквивалентного конфокального резонатора или к анализу возмущенной конфокальной системы. [38]

Из рассмотренных до сих пор соотношений, связанных с представлением распределения поля конфокального резонатора на рис. 2.9, б, легко видеть, что в рамках использованных приближений для каждого резонатора можно найти эквивалентный конфокальный резонатор. Конфокальный резонатор на рис. 2.9, б построен таким образом, что в определенных местах ( z L / 2 Ri / 2) гауссова пучка расположены зеркала, радиус кривизны которых равен радиусу кривизны волнового фронта светового пучка. Из условия самосогласованности явствует, что введение зеркал не изменяет заданного распределения напряженности поля в гауссовом пучке. Мы можем также вместо конфокальных зеркал поместить зеркала в других местах оси г. Они не изменят распределения поля, если их радиус кривизны будет равен радиусу кривизны волнового фронта в соответствующем месте. При этом схема не должна быть симметричной. Поскольку все эти различные схемы резонаторов приводят к одному и тому же распределению поля, их называют эквивалентными. [39]

Формула (2.73) дает дальнопольное распределение излучения р, / - и моды конфокального резонатора. [40]

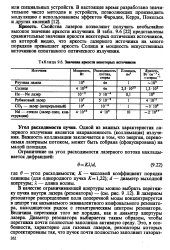Значения яркости некоторых источников. [41]

В лазерном резонаторе распределение поля поперечной моды концентрируется в центре так называемого эквивалентного конфокального резонатора, находящегося рядом с геометрическим центром резонатора. [42]

& - конфокальное расстояние; 2 0 /; о - расстояние от центра конфокального резонатора до рассматриваемой поверхности; х и г / - расстояния, измеряемые в плоскости, перпендикулярной оси резонатора. [43]

В основе метода ЭКР лежит предположение о том, что поле рассматриваемого произвольного резонатора совпадает с полем эквивалентного конфокального резонатора. [44]

В заключение отметим, что для резонатора другой формы, например, для цилиндрического, эллиптического или конфокального резонатора, модовые функции имеют другой вид. Тем не менее, благодаря граничным условиям (10.24), волновые числа принимают дискретные значения. [45]

Страницы: 1 2 3 4