Результат - измерение - теплоемкость
Cтраница 2
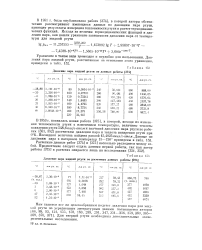
В статье Аристова, Безуса, Березина и Си-ницына [1] приведены результаты измерений теплоемкости адсорбированных на графитированной саже бензола и и-гексана в широкой области заполнений поверхности при 293 К. Нами совместно с А. В. Киселевым и А. Я. Афреймовичем были проведены молекулярно-статистические расчеты дифференциальных изменений теплоемкости Дс0, бензола [2], метана, этана, пропана [3], к-бутана и к-пентана [4] при переходе из объема газа в адсорбированное состояние на базисной грани графита при низких заполнениях поверхности. Результаты расчетов ДСОА для этана, пропана, w - бутана и к-пентана ( в качестве силовых центров молекул приняты звенья СН3 и СН2 и использованы эффективные потенциальные функции для взаимодействия этих силовых центров с поверхностью) приведены на рисунке. [16]
Уравнение (3.58) широко используется для определения зависимости V от Т по результатам измерения теплоемкости Ср и наоборот. [17]
В статье Аристова, Безуса, Березина и Си-ницына Ц ] приведены результаты измерений теплоемкости адсорбированных на графитированной саже бензола и н-гексана в широкой области заполнений поверхности при 293 К. Нами совместно с А. В. Киселевым и А. Я. Афреймовичем были проведены молекулярно-статистические расчеты дифференциальных изменений теплоемкости Дс, бензола [2], метана, этана, пропана [3], к-бутана и и-пентана [4] при переходе из объема газа в адсорбированное состояние на базисной грани графита при низких заполнениях поверхности. Результаты расчетов Дс0) д для этана, пропана, w - бутана и к-пентана ( в качестве силовых центров молекул приняты звенья СН3 и СН2 и использованы эффективные потенциальные функции для взаимодействия этих силовых центров с поверхностью) приведены на рисунке. [18]
Уравнение (2.100) широко используется для определения зависимости объема V от р, Т по результатам измерения теплоемкости CJ:, и наоборот. [19]
Уравнение ( 4 - 64) широко используется для определения зависимости V от Т по результатам измерения теплоемкости Ср и наоборот. [20]
Впервые стандартная энтропия газообразного трехфтористого бора была определена в работе Эйкена и Шредера [1505] в результате измерения теплоемкости BF3 от 12 до 173 К. [21]
Уравнение ( 3 - 57) широко используется для определения зависимости 1 / от Т по результатам измерения теплоемкости С, и наоборот. [22]
Ставшие в последнее время многочисленными исследования свойств так называемых пластических кристаллов могут служить другим примером работ, в которых результаты измерения теплоемкости используются для изучения фазовых переходов. [23]
Энтропия ряда газов была вычислена с применением суммы состояний, и полученные величины сравнивались со значениями, вычисленными на основании результатов измерения теплоемкости. В последнем случае вычисление величины энтропии ведется с применением третьего закона термодинамики, утверждающего, что энтропия твердого тела при абсолютном нуле равна нулю. [24]
 |
Давление пара жидкой ртути по расчетным данным работы. [25] |
В 1951 г. была опубликована работа [374], в которой авторы обстоятельно рассматривают имеющиеся данные по давлению пара ртути, приводят результаты измерения теплоемкости ртути и расчет термодинамических функций. [26]
В температурном интервале, доступном для ртутного термометра, теплоемкость большинства веществ довольно медленно увеличивается с ростом температуры, поэтому при отнесении результатов измерения теплоемкости к определенной температуре не требуется очень высокой точности измерения последней. Так же как и в случае определения тепловых эффектов реакций, измерение температуры в Международной шкале с точностью 0 1 практически всегда является достаточным. [27]
Нейлсон и Уайт [3037] вычислили 5 g250 ( СНР2С1, газ) 63 92 0 28 кал / моль град на основании полученных ими результатов измерений теплоемкости и теплот фазовых переходов дифторхлорметана. Найденное в работе [3037] значение S 32 50 ( CHF2C1, газ) находится в согласии со значением 64 05 кал / моль - град этой величины, вычисленным по принятым в Справочнике молекулярным постоянным CHFaCl. Теплоемкости паров дифторхлорметана н фтордихлорметана были измерены Беннигом и Мак-Харнессом [744] при давлении в 1 атм в интервалах температуры 322 2 - 408 3 К для CHF2C1 и 288 9 - 408 3 К для СНРСЬ. [28]
Согласно расчетам Гуина и Питцера [556] на основании низкотемпературных данных S 29g ( g) 73 66 кал / ( моль - К); эти исследователи опубликовали также результаты измерения теплоемкости пара. Теплоемкость идеального газа рассчитана для ряда температур из спектроскопических данных с использованием потенциальной функции для внутреннего вращения, подобранной таким образом, чтобы соответствовать экспериментальным результатам. Сглаженная кривая, проведенная на основании как экспериментальных, так и расчетных точек, использована для определения приведенных здесь значений. [29]
Незначительное расхождение ( менее 1 кДж / моль в величинах A f и AGf и менее 2 Дж / град-моль в величинах ASf и 5 298 15ЬпРз) в термодинамических данных, приведенных в табл. 2 и 3, по сравнению с ранее опубликованными [ 30 - 32 и 34 ] вызвано тем, что для LaF3, PrF3, NdF3, GdF3 и LuF3 величины Яг - Яг 298 и ST - - S 29s, использованные в данной работе, брались не по [ 26 и 27 ], как делалось нами раньше, а согласно [ 9 и 45 ], где данные работ [ 26 и 27 ] были приведены в соответствие с результатами измерения теплоемкости указанных фторидов при низких температурах. [30]
Страницы: 1 2 3 4