Классический результат

Cтраница 2

Вслед за классическим результатом Понтрягина и Куратовского были предложены другие критерии планарности. [17]

Таким образом, классический результат ( Newcomb, 1958) для идеальной плазмы, что сохранение потока ( а) означает сохранение линии ( б) также выполняется в неидеальной плазме. Однако в неидеальном случае сохранение линии необязательно означает сохранение потока. [18]

Эта теорема усиливает классический результат Боннэ, где речь идет об отрезке геодезической, кратчайшем в сравнении с достаточно близкими к нему линиями. В теореме А. В. Погорелова последнее требование снимается. [19]

II представлены некоторые классические результаты теории аналитических полугрупп, а также сравнительно недавние результаты Да Нрато и Гривара, связывающие теорию интерполяции в банаховых пространствах и теорию аналитических полугрупп. [20]

Отметим ниже несколько классических результатов, которые могут быть получены без труда. [21]

Методы получения некоторых классических результатов являются оригинальными. В частности, в самом общем виде получены уравнения движения непрерывно распределенных источников внешних полей как следствие уравнений Эйнштейна и уравнений соответствующих полей. [22]

Для полупространства кроме классических результатов приведены решения некоторых нетрадиционных контактных задач. [23]

Первый отдел посвящен классическим результатам, относящимся к задаче кручения и изгиба однородных брусьев ( решение задачи растяжения в этом случае тривиально) и принадлежащим в основном Сен-Венану. [24]

Незнакомые с этими классическими результатами люди могут думать, что участвовать в любой невыгодной игре неразумно. [25]

По сравнению с классическими результатами первых трех параграфов результаты § 4.4 относительно новы. Они связаны с теоремой А. Стоуна о возможности вписать локально конечное подпокрытие в любое открытое покрытие метризуемого пространства и дают топологические условия, характеризующие метризуемость, и условия сохранения метризуемости при отображениях. [26]

Теарема Шаудера является известным классическим результатом. [27]

Следует подчеркнуть, что классические результаты [11] в теории п-ортогональных криволинейных систем координат носили в основном классификационный характер и были недостаточно эффективны для построения явных примеров. Как следствие список явных примеров таких координат был весьма невелик. [28]

С его помощью воспроизведены классические результаты для диаграмм с одной петлей1); это рассмотрение аналогично приведенному для интеграла унитарности в § 7 гл. Стоит отметить, что Фотиади и Фам работают с компонентами 4-им-пульсов. Из теоремы Холла - Вайтмана следует, что при переходе к инвариантам ( Pi Pj) 2 не появляется никаких дополнительных особенностей. [29]

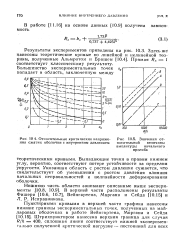Относительные критические напряже - Рис Значения от-ния сжатия оболочки с внутренним давлением носительной величины. [30]

Страницы: 1 2 3 4