Главное значение - интеграл
Cтраница 1
Главное значение интеграла, стоящего под знаком суммы, вычисляется просто ( см. стр. [1]
Главные значения интеграла в смысле Коши, используемые в определении преобразования Гильберта и сингулярных сверток типа Кальдерона - Зигмунда, имеют именно такой вид. [2]
Главными значениями интегралов широко пользуются в теории интегралов Фурье, операционном исчислении и многих других разделах математики. [3]
Понятие главного значения интеграла может быть определено и в случае криволинейного интеграла. [4]
Понятие главного значения интеграла может быгь определено и в случае криволинейного интеграла. [5]
При определении главного значения расходящегося TV-кратного интеграла вместо стягивающихся последовательностей кругов берутся стягивающиеся последовательности TV-мерных шаров. [6]
Имеется в виду главное значение интеграла с исключением особой точки. [7]
Аналогично можно определить главное значение интеграла в случае бесконечных пределов интегрирования. [8]
Совершенно аналогично определяется главное значение интеграла и в том случае, когда f ( х) имеет несколько точек разрыва непрерывности внутри промежутка. Если существует обычный несобственный интеграл от функции f ( х) по всему промежутку ( а, Ь) [ I, 97 ], то главное значение интеграла ( 150) совпадает, очевидно, с этим несобственным интегралом. Из определения ( 150) непосредственно вытекает, что постоянный множитель можно выносить за знак интеграла и что интеграл от суммы конечного числа слагаемых равен сумме интегралов от отдельных слагаемых, причем предполагается, что интегралы от слагаемых существуют в смысле главного значения. [9]
Совершенно аналогично определяется главное значение интеграла и в том случае, когда f ( x) имеет несколько точек разрыва непрерывности внутри промежутка. Если существует обычный несобственный интеграл от функции / ( х) по всему промежутку ( а, Ь [ I, 97), то главное значение интеграла ( 145) совпадает, очевидно, с этим несобственным интегралом. Из определения ( 145) непосредственно вытекает, что постоянный множитель можно выносить за знак интеграла и что интеграл от суммы конечного числа слагаемых равен сумме интегралов от отдельных слагаемых, причем предполагается, что интегралы от слагаемых существуют в смысле главного значения. [10]
Заметим, что главное значение интеграла совпадает с обычным ( собственным или несобственным) интегралом, если этот последний существует. [11]
Это относится к главным значениям интегралов. В точках же х О каждый из интегралов независимо от соотношения между 2т и П обращается в оо и их разность равна нулю. [12]
Здесь Р - символ главного значения интеграла и предполагается, что У. [13]
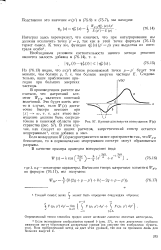 |
Кривые для энергии возмущения W ( x. [14] |
Определенный таким способом предел носит название главного значения интеграла. [15]
Страницы: 1 2 3