Точное значение - интеграл
Cтраница 1
Точное значение интеграла зависит от конструкции 8-функции. [1]
Точное значение интеграла остается довольно часто неизвестным. Практическое значение остаточных членов невелико. В связи с этим возможность определения точности результатов, полученных по формулам численного интегрирования, приобретает особое значение. [2]
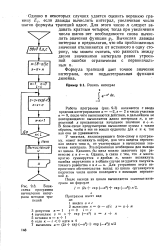 |
Блок-схема программы вычисления интеграла методом трапеций. [3] |
Формула трапеций дает точное значение интеграла, если подынтегральная функция линейна. [4]
При этом можно, пользуясь т ординатами, получить точное значение интеграла, если под интегралом-целая, рациональная функция 2т - го порядка; для любой другой функции это будет приближенное выражение интеграла, соответствующее приближенной замене подинтегральной функции полиномом 2т - й степени. Определяя таким способом потенциальное обтекание эллиптического цилиндра, можно получить при системе четырех линейных уравнений с четырьмя неизвестными результат, совпадаюший с точным в пяти-шести знаках. [5]
Найти 8 / - /, где / - точное значение интеграла, а - / - его приближенное значение, вычисленное с шагом / 1 2 по формуле: а) прямоугольников; б) трапеций; в) Снмпсона. [6]
Если удается с помощью формулы Ньютона - Лейбница найти точное значение интеграла, то полезно сравнить с ним результат приближенного вычисления. [7]
Стремится ли сумма ( 3) при п-со к точному значению интеграла, и если стремится, то с какой скоростью. [8]
Найти в - / - /, где / - точное значение интеграла, а - У - его приближенное значение, вычисленное с шагом h 2 по формуле: а) прямоугольников; б) трапеций; в) Симпсона. [9]
Хотя за последнее время были достигнуты большие успехи в вычислении точного значения интегралов такого типа, все же полуэмпирический метод вычисления Р продолжает давать очень ценные результаты. [10]
В рассмотренном примере погрешность численного интегрирования легко оценивалась, поскольку имелось точное значение интеграла. [11]
Симпсона с h - 1 и метод Гаусса с двумя ординатами позволяют вычислить точное значение интеграла, хотя при использовании метода Гаусса требуется одной ординатой меньше по сравнению с формулой Симпсона. [12]
В зависимости от числа узловых точек изменяется степень полинома, для которого формула дает точное значение интеграла, так как при добавлении одной точки его степень увеличивается на два. [13]
Ответ в методе статистических испытаний носит вероятностный характер и в принципе может сколь угодно сильно отличаться от точного значения интеграла. [14]
Читатель, конечно, дает себе отчет в том, что погрешность мы смогли оценить здесь лишь потому, что наперед знали точное значение интеграла. Для того чтобы наши формулы были действительно пригодны для приближенных вычислений, нужно иметь удобное выражение для погрешности, которое позволяло бы не только оценивать погрешность при данном п, но и выбирать п, обеспечивающее требуемую степень точности. [15]
Страницы: 1 2 3