Приближенное значение - интеграл
Cтраница 2
Пусть ( - щ) - уровень надежности, с которым желательно получить приближенное значение интеграла, е - заданная точность. [16]
Если вместо того, чтобы интегрировать исходное дифференциальное уравнение обычным методом и затем находить приближенное значение интеграла, пользоваться методом интерполяции, в частности методом трапеций, то получим формулу, данную проф. [17]
Эта формула описывает хорошо известное правило трапеций для численного интегрирования; согласно этому правилу, приближенное значение интеграла (6.1) получается в виде суммы площадей п трапеций. [18]
Продолжая процесс уменьшения шага интегрирования вдвое, приходим к формуле (5.37), по которой каждое новое приближенное значение интеграла (5.36) получаем, вычислив дополнительно подынтегральную функцию только в 2 узле. [19]
Даже в тех случаях, когда известна первообразная, на практике бывает иногда более удобно находить приближенное значение интеграла не по формуле Ньютона-Лейбница, а по формулам приближенного интегрирования. [20]
 |
Программа, позволяющая переупорядочить массивы X и Y так, чтобы значения X шли в порядке возрастания. [21] |
Если окажется, что значения X расположены на равном расстоянии друг от друга с шагом Н, то приближенное значение интеграла можно найти с помощью метода трапеций, знакомого читателям из гл. [22]
Когда и принимает не слишком малые положительные значения, то, как мы видели выше, мы можем получить приближенное значение интегралов Френеля при помощи разложения в полусходящиеся ряды. [23]
Известно, что основное назначение и практическая ценность различных способов приближенного интегрирования заключается в том, что они позволяют находить приближенное значение интеграла, не поддающегося точному вычислению. Однако мы ограничимся решением некоторых примеров, где точное значение интеграла легко находится и где мы можем сравнить полученное нами приближенное значение с точным. [24]
Таким образом, для приближенного вычисления определенного интеграла нужно выбрать подходящую формулу, позволяющую по имеющейся о функции информации находить приближенное значение интеграла, и оценить погрешность, которую дает эта формула. [25]
В задачах 1187 - 1190 по методу Эйлера на указанном отрезке, разделяя его на 10 равных частей, составить таблицу приближенных значений интеграла данного уравнения, удовлетворяющего указанному начальному условию. [26]
Прием многократного удвоения числа элементарных отрезков и оценки погрешности можно запрограммировать и получить метод, который автоматически определяет элементарные отрезки так, чтобы приближенное значение интеграла вычислялось с предписанной точностью. [27]
Тогда из сопоставления вычислений по двум формулам мы и получим возможность судить о величине ошибки, так как одно из получаемых таким образом приближенных значений интеграла будет больше, а другое меньше истинного. [28]
Выше мы уже обрисовали картину, складывающуюся при вычислении интегралов большой кратности, как почти полностью безнадежную в случае, если ставится цель получения приближенного значения интеграла с гарантированно малой оценкой погрешности. Такая обстановка и вызвала к жизни применение метода Монте-Карло. [29]
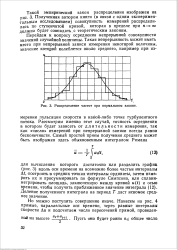 |
Распределение частот при нормальном законе. [30] |
Страницы: 1 2 3 4