Приближенное значение - интеграл
Cтраница 3
А /, построить ( в средних точках интервалы ординаты, затем измерить их и просуммировать по формуле Симпсона, или сплани-метрироозать площадь, заключенную между кривой u ( t) и осью времени, чтобы получить приближенное значение интеграла ( 12), Деление полученного интеграла на период Т даст искомое среднее значение. [31]
В программе 5.1 F метод средних прямоугольников оформлен в виде подпрограммы RECT, имеющей входные параметры: А, В - пределы интегрирования; N - число разбиений интервала интегрирования; F - имя подпрограммы для вычисления подынтегральной функции и выходной параметр; S - приближенное значение интеграла. Введение имени F в число формальных параметров позволяет составлять программы, включающие вычисление интегралов от нескольких различных функций. В вызывающей программе имена подпрограмм всех подынтегральных функций должны быть включены в оператор EXTERNAL. Порядок Р и аргумент функции Бесселя Z передаются в подпрограмму-функцию F ( X) через неименованный COMMON-блок. [32]
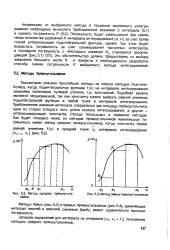 |
Метод левых прямоугольников. [33] |
Рассмотрим сначала простейшие методы из класса методов Ньютона-Котеса, когда подынтегральную функцию f ( x) на интервале интегрирования заменяем полиномом нулевой степени, т.е. константой. Приближенное значение интеграла определится как площадь прямоугольника, одна из сторон которого есть длина отрезка интегрирования, а другая - аппроксимирующая константа Отсюда происходит и название методов. [34]
Рассмотрим теперь некоторые способы приближенного интегрирования функций. Формулы для приближенных значений интегралов называются квадратурными формулами. [35]
В приведенной ниже программе для интегрирования методом Эйлера с помощью бесконечного цикла число интервалов удваивается после каждой итерации. Каждое из вычисленных приближенных значений интеграла вы можете увидеть на экране и, сравнивая их, решить, удовлетворяет ли вас полученный результат. [36]
Обычно берут Aj / A2 2; процесс вычислений заканчивается, когда Т С е, где е - заданная точность. Этот способ получения приближенного значения интеграла может быть использован для составления программ с автоматическим выбором шага интегрирования. [37]
Если это условие выполнено, то за приближенное значение интеграла по G принимается значение, вычисленное по кубатурной формуле Qfi обычно являющейся линейной комбинацией формул QI и Q - Если условие ( 5) не выполняется, то куб G разбивается на 2s равных кубов и описанный алгоритм применяется к каждому из этих кубов. Процесс дробления продолжается до тех пор, пока условие ( 5) не будет выполнено. Если при делении шага h пополам наступит такой момент, когда hs станет машинным нулем, то счет прекращается. Используемые в стандартных программах кубатурные формулы Qsq имеют следующий вид. [38]
Для оценки погрешности, кроме ( 5), ( 9), ( 12), используют еще правило Рунге, которое в простейшем виде состоит в следующем. Пусть J k, / 2 и Jtk - приближенные значения интеграла /, полученные при делении отрезка интегрирования на k, 2k и 4k частей. [39]
Для оценки погрешности, кроме ( 5), ( 9), ( 12), используют еще правило Рунге, которое в простейшем виде состоит в следующем. Пусть J /, J % k и J k - приближенные значения интеграла J, полученные при делении отрезка интегрирования на &, 2k и 4& частей соответственно. [40]
Широко распространено мнение, что так как методы квадратур Гаусса столь хороши, они чувствительны к незначительным ошибкам. Небольшое рассуждение показывает, что если узел задан с ошибкой, то приближенное значение интеграла изменяется на величину этой ошибки, умноженную на производную подынтегральной функции и вес в этом узле. То же самое, конечно, верно для любого метода интегрирования. Тот факт, что все веса гауссовой квадратуры положительны, обеспечивает для нее отсутствие интерференции. [41]
Поэтому применение метода Монте-Карло вызвано обстановкой, когда трудно надеяться на получение приближенного значения интеграла с гарантированно малой оценкой погрешности. [42]
Блок-схема ( схема 4) в своем ядре содержит цикл FOR-NEXT, в котором для N интервалов вычисляется интегральная сумма. Во внешнем бесконечном цикле число интервалов удваивается после каждого прохождения внутреннего цикла и текущее значение суммы ( приближенное значение интеграла) выводится на экран. [43]
Пусть имеется какой-то способ интегрирования, где информация о подынтегральной функции учитывается лишь в виде информации о ее значениях в отдельных точках. Этот способ определяется заданием первого узла интегрирования, правила, по которому отыскиваются следующие УЗЛЫ, и способа вычисления приближенного значения интеграла. [44]
Но построение такого инструмента, который позволял бы приближенно вычислить данный интеграл с любой степенью точности, дается нам уже в самом определении понятия интеграла. Производя достаточно 1мелкое разбиение основного отрезка и составляя для этого разбиения вышеупомянутые суммы, мы, очевидно, и получим приближенное значение интеграла с любой наперед заданной степенью точности. Таким образом, в принципиальном плане исчерпывающий метод вычисления интеграла дается уже самим его определением. И если мы тем не менее всегда искали и впредь будем искать других методов, ведущих к этой цели, то это лишь потому, что в практическом плане этот прямой метод в большинстве случаев оказывается неприменимым по своей чисто технической сложности и трудоемкости. [45]
Страницы: 1 2 3 4