Отрицательное собственное значение

Cтраница 3

Если все собственные значения положительны или если имеется только конечное число отрицательных собственных значений, то будет справедлив. [31]

По теореме Сильвестра число отрицательных диагональных элементов матрицы РТСР равно числу отрицательных собственных значений матрицы С. Это число называется степенью неустойчивости системы. [32]

Итак, знаки главных миноров симметричной матрицы позволяют установить число ее положительных и отрицательных собственных значений. [33]

Согласно сказанному выше число положительных и отрицательных элементов D равно соответственно числу положительных и отрицательных собственных значений матрицы А. Но элементы матрицы D легко определить. [34]

Но чтобы по знакам главных миноров Л Е правильно определить число ее нулевых, положительных и отрицательных собственных значений, необходимо быть уверенным, что Л Е является матрицей Якоби. Не каждый вычислительный процесс гарантирует выполнение обоих условий одновременно. [35]

По предположению, матрица Грама Go подпространства имеет как положительные, так и отрицательные собственные значения. [36]

Покажем, наконец, что статистический оператор положительно определен, т.е. не имеет отрицательных собственных значений. [37]

Покажем теперь, что всем собственным функциям, отличным от рассмотренных выше, соответствуют отрицательные собственные значения. Для этого умножим обе части уравнения ( 12.2) на 4 ( ы) ( где Ч - любая собственная функция, отличная от линейной комбинации величин 1, и, и. [38]

Пусть дан эрмитов оператор L с дискретным спектром, содержащим не более конечного числа отрицательных собственных значений ( пп. [39]

Так как Rm ориентируемо, то матрица С может иметь толь: четное число отрицательных собственных значений. [40]

Пусть дан эрмитов оператор L с дискретным спектром, содержащим не более конечного числа отрицательных собственных значений ( пп. [41]

В частности, его ось будет направлена вдоль того собственного вектора, который соответствует отрицательному собственному значению. [42]

Задаче - у Я ( sgn x у. у ( 1. [43]

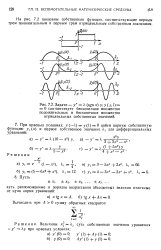
На рис. 7.2 показаны собственные функции, соответствующие первым трем положительным и первым трем отрицательным собственным значениям. [44]

Если квадратическая аппроксимация адекватно описывает поверхность, то формула (6.62) приводит к максимуму при отрицательных собственных значениях и к минимуму при положительных собственных значениях. [45]

Страницы: 1 2 3 4