Наименьшее собственное значение

Cтраница 1

Наименьшее собственное значение Я определяется формулой ( 24), а величина коэффициента k дается графиком фиг. [1]

Здесь наименьшее собственное значение А, 5 является двукратно вырожденным, ему соответствуют две линейно независимые собственные функции У. [2]

Наименьшее собственное значение стационарного оператора переноса ( см. § 2.4) определяет также критичность ядерного реактора, а соответствующая собственная функция - плотность нейтронов в реакторе в критическом состоянии. [3]

Итак, наименьшее собственное значение гамильтониана Н для состояний заданного типа является абсолютным минимумом величины Е как функционала от пробных функций этого типа. Наоборот, если используются лишь пробные функции данного типа, то Е всегда есть верхняя граница для такого наименьшего собственного значения. [4]

При возрастании п наименьшее собственное значение К [ п) матрицы (0.3), именуемое обычно мерой линейной независимости п первых элементов системы (0.1), не возрастает, а наибольшее собственное значение Я п этой матрицы не убывает. [5]

А, - наименьшее собственное значение набора, v0 - основная частота системы и Ф - любая функция, удовлетворяющая граничным условиям садачи. Интегрирование производится здесь по всей колеблющейся зистеме, a dr - элемент объема, определенный и охарактеризованный на стр. [6]

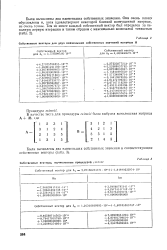Собственные векторы для двух наименьших собственных значений матрицы Н. [7]

Были вычислены два наименьших собственных значения. Они очень плоха обусловлены и, хотя удовлетворяют некоторой близкой возмущенной матрице, не очень точны. [8]

Если ц-приближение к наименьшему собственному значению, а т) очень мало, то (5.1.4) дает вполне удовлетворительный результат. [9]

Пусть А 0 - наименьшее собственное значение, a v ( г; 1) - соответствующий ему собственный вектор матрицы Вт В. [10]

Таким образом, если наименьшее собственное значение К0 положительно, то функция Грина А 1 ( х, г) нигде не обращается в нуль. [11]

Таким образом, определены наименьшее собственное значение EQ и связанная с ним собственная функция Ф0 гамильтониана гармонического осциллятора. [12]

В приложениях часто требуется найти наименьшее собственное значение, и тогда автоматически выбирается обратный степенной метод. [13]

Но для краевых условий (5.17) наименьшее собственное значение AI равно нулю и ему отвечает собственная функция HI const, в чем можно убедиться непосредственно. [14]

При данном 12 надо взять наименьшее собственное значение оператора Л2, которое соответствует самому долгому времени релаксации. [15]

Страницы: 1 2 3 4