Соответствующее экспериментальное значение
Cтраница 1
Соответствующие экспериментальные значения обозначены Pij. Уточнения проводились методом оврагов [94] по данным опытов, приведенных в табл. VI.8. Таким образом, удавалось определить константы, не допуская при этом погрешности, обусловленной линеаризацией начальных участков кинетических кривых. В следующей работе [95] для уточнения значений констант, найденных из планированных экспериментов, использовались кинетические кривые, снятые в широком диапазоне времен контакта. [1]
Соответствующие экспериментальные значения либрационных частот v / в Н2О и в D2O в твердой фазе, а также в жидкой при 10 С приблизительно обратно пропорциональны значениям квадратных корней из средних моментов инерции легкой / н и тяжелой / о молекул относительно осей либрации. [2]
Соответствующие экспериментальные значения либрационных частот гг в Н20 и в D20 в твердой фазе, а также в жидкой при 10 С приблизительно обратно пропорциональны значениям квадратных корней из средних моментов инерции легкой / н и тяжелой / Е молекул относительно осей либрации. [3]
В то же время соответствующие экспериментальные значения равны: Эксп. [4]
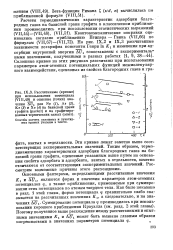
Горизонтальная пунктирная линия показывает соответствующее экспериментальное значение К. [5]
Эти кривые лежат заметно выше соответствующих экспериментальных значений. Таким образом, термодинамические характеристики адсорбции благородных газов на базисной грани графита, оцененные указанным выше путем на основании свойств адсорбата и адсорбента, взятых в отдельности, заметно отличаются от соответствующих экспериментальных значений. Рассмотрим возможные причины этого расхождения. [7]
Рассчитанные кривые лежат заметно ниже соответствующих экспериментальных значений. В этом случае, как и в случае выбора атомов С и Н в качестве силовых центров молекулы, можно предположить, что основной причиной расхождения рассчитанных и опытных значений KI является погрешность в значениях параметров С для межмолекулярных взаимодействий силовых центров СН4, СН3 и СН2 с атомом С графита. [8]
Рассчитанные по Борну величины ДЯзеоли значительно превышают соответствующие экспериментальные значения. [9]
Эти вычисленные значения могут быть сопоставлены с соответствующими экспериментальными значениями. [10]
Хараша показывает, что отклонения расчетных значений от соответствующих экспериментальных значений не превышают 6 ккал / моль. [11]
Рассчитанные значения К находятся в хорошем согласии с соответствующими экспериментальными значениями. Рассчитанные, как и экспериментальные, значения Ki для фенантрена меньше, чем для антрацена. [13]
Рассчитанные по Борну величины ДЯ СОЛИ) значительно превышают соответствующие экспериментальные значения. Это указывает на весьма приближенный характер допущений, положенных в основу модели Борна. Поэтому были предприняты неоднократные попытки уточнить теорию сольватации Борна. В модели ван - Аркеля и де - Бура при расчете энергии сольватации использовался следующий воображаемый цикл: а) испарение п молекул растворителя, необходимых для образования первичной сольватной оболочки ( обычно п4 - - 8); б) взаимодействие иона в газовой фазе с п молекулами растворителя, которое приводит к образованию заряженной сферы с радиусом гг 2г8, где rs - радиус молекулы растворителя; в) внесение образовавшейся сферы в растворитель по модели Борна. Аналогичный цикл рассматривался также в модели Эли и Эванса, которые, однако, учитывали тетраэдрическую структуру воды и водных растворов: а) удаление из воды одного тетраэдра, состоящего из пяти молекул Н2О; б) разрушение этого тетраэдра в вакууме; в) построение из иона и четырех молекул Н2О нового заряженного тетраэдра; г) внесение заряженного тетраэдра в полость, оставшуюся от удаленного тетраэдра из пяти молекул Н2О; д) конденсация оставшихся в вакууме молекул воды. [14]
 |
Зависимость критического коэффициента интенсивности напряжений при динамическом нагруже-нии KID от скорости роста трещины v. [15] |
Страницы: 1 2 3 4 5