Среднее значение - поле
Cтраница 1
Среднее значение конденсат-ного поля в ядре с равным нулю моментом равно нулю. Отличен от нуля только средний квадрат конденсатного поля. [1]
При этом среднее значение поля р равно нулю. [2]
 |
Блок-схема измерителя напряженности магнитного поля ИМИ-1. [3] |
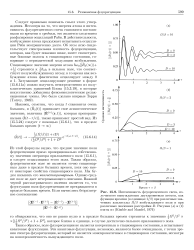
При совпадении среднего значения поля Я с резонансным значением моделирующего поля дважды за период проходит резонансное поглощение, при этом осуществляется амплитудная модуляция колебаний высокочастотного контура. После детектирования ( 2) и усиления ( 3 сигнал подается на осциллограф 4, где является функцией постоянного поля. [4]
При совпадении среднего значения поля Н0 с резонансным значением моделирующее поле дважды за период проходит резонансное поглощение, осуществляя при этом амплитудную модуляцию высокочастотных колебаний. [6]
Из этой формулы видно, что среднее значение поля флуоресценции прямо пропорционально собственному значению оператора приложенного поля (15.6.1), и следует осцилляциям этого поля. Таким образом, флуоресцентное поле не является точно стационарным даже в пределе больших времен, хотя оно имеет некоторые свойства стационарного поля. [8]
Приближенность приведенного расчета определяется тем - что мы взяли среднее значение поля, создаваемого первой молекулой, а не провели детального расчета вероятности различных взаимных ориентации дипольных моментов. [9]
Приближенность приведенного расчета определяется тем, что мы взяли среднее значение поля, создаваемого первой молекулой, и не провели детального расчета вероятности различных взаимных ориентации дипольных моментов. [10]
Неплохая оценка F получается, если учесть, что среднее значение хиггсовского поля зависит от температуры. [11]
Состав рудовмещающих пород позволяет считать наиболее перспективными ячейки со средними значениями поля. [12]
Неплохая оценка Jf ph получается, если учесть, что среднее значение хиггсов-ского поля зависит от температуры. Эта температурная зависимость ( Киржниц, 1972; Киржниц, Линде, 1972; Долан, Джекив, 1974; Вайнберг, 1974) исследуется методами, далеко выходящими за рамки данной книги. [13]
Для парамагнитных веществ хт не зависит от поля ( для слабых и средних значений поля) и уменьшается в сильных полях при приближении к насыщению. Теория, объясняющая эти факторы, построена для газов Ланжевеном на основании предположения, что атом парамагнитного газа обладает постоянным магнитным моментом. При помещении в магнитное поле все атомные волчки начнут совершать прецессионные движения вокруг вектора намагничивающего поля, что поведет к появлению диамагнитного эффекта. Однако если прецессионное движение будет чем-либо ( например вследствие взаимных столкновений молекул) заторможено, то все магнитные моменты атомов повернутся в направлении намагничивающего поля, и тело намагнитится до насыщения. При всякой другой t установится нек-рое подвижное равновесие между упорядочивающим действием намагничивающего поля и дезорганизующим действием тепловых столкновений. Ланжевен произвел этот подсчет, пользуясь методами кинетич. [14]
При г 0 потенциал U - a / HI, где Н - некоторое среднее значение поля на оси z, в точке D U к, - а / Но, а в точках А и 5, лежащих на штриховой силовой линии, потенциал U логарифмически ( поскольку в точке А поле линейно обращается в нуль) стремится к - сю. Как мы видим, потенциал U имеет яму на силовой линии, проходящей через точку А, где поле обращается в нуль. Тогда из рис. 2 следует, что любое такое расположение плазмы, когда ее давление убывает в направлении от штриховой силовой линии, наверняка является устойчивым. [15]
Страницы: 1 2 3 4