Среднее значение - поле
Cтраница 4
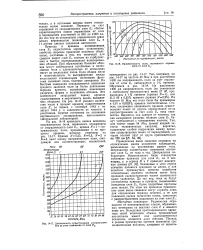 |
Длительность существования распространения за счет отражения от слоя Ес.| Напряженность поля, вызванного отражением от слоя Е. [46] |
При образовании больших обла-крв могут наблюдаться устойчивые и интенсивные поля с длительностью от нескольких минут до нескольких часов. Если облака малы и многочисленны, то интерференция между несколькими отраженными волновыми фронтами вызывает очень быстрые замирания. На быстрые замирания накладываются изменения среднего значения поля за более длительные периоды времени, вызываемые изменением размеров, формы и положения облаков. Эти особенности затрудняют оценку времени существования и вероятности помех, вызываемых облаками. Кривые построены на основании вертикального зондирования, выполненного Центральной лабораторией. [47]
Оба эти оператора представляют собой сумму одноэлектронных сферически симметричных операторов, поэтому вычисление их средних значений проводят так же, как и для среднего значения экранирующего поля. [48]
В районах многолетней мерзлоты различие в электрических и упругих свойствах между рыхлыми и коренными породами мало, поэтому определение погребенного рельефа в мерзлой толще геофизическими методами затруднено. Усложняется характер гравитационного и магнитного поля за счет жильных льдов среди мерзлых пород, что приводит к появлению отрицательных аномалий Ag и AZ. Влияние подобных аномалий может быть исключено путем групповых измерений ( 25 - 30) на площади круга с радиусом в 10 - 15 м для получения среднего значения поля. Толщи мерзлых пород при работах сейсморазведкой методом преломленных волн ( МПВ), электроразведкой на постоянном токе, эманационной съемкой и другими методами часто являются экранирующими. [49]
Наиболее общим способом описания взаимодействия оптического излучения с веществом, как известно, являются уравнения Максвелла. Однако непосредственный переход от уравнений Максвелла к томографии в настоящее время вряд ли возможен. Поэтому необходима промежуточная более простая математическая модель, не обязательно самая точная, но обязательно позволяющая осуществить переход к томографии. Использование статистического подхода и аппарата корреляционных функций [84] позволяет получить уравнения Дайсона для средних значений поля и Бете-Солпитера для вторых моментов. Хотя практически эти уравнения бесполезны из-за невозможности их решения, они дают возможность обоснования уравнения переноса излучения ( УПИ) [85], являющегося наиболее популярным инструментом как при описании прохождения излучения через СРС, так и в качестве основы для перехода к томографии. [50]
Наличие беспорядочных пульсаций в течениях жидкости и газа ( именуемое турбулентностью) делает мало реальным изучение индивидуальных полей турбулентных движений. Это обстоятельство определяет интерес к статистическому описанию этих течений, что было ясно основателю теории турбулентности О. Однако предложенное им простейшее усреднение по заданному интервалу времени ( или же по некоторой области пространства) оказалось не слишком удобным ввиду трудности получения достаточно простых и надежных уравнений для средних значений поля скоростей. [51]
Поле Ф от источника J изменяет состояние виртуальных вакуумных частиц, взаимодействующих с этим полем. Поскольку квантовый процесс возникновения и уничтожения виртуальных пар имеет случайный характер, то мгновенное значение поля Ф не совпадает с его средним значением Ф); поле испытывает квантовые флуктуации. Поэтому само описание поля в терминах его средних значений имеет ограниченную область применимости. Это описание пригодно в той ситуации, когда квантовые флуктуации малы по сравнению со средним значением поля. [52]
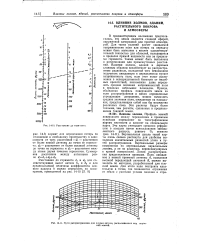 |
Пути распространения для случая антенн, расположенных над неровной землей. [53] |
В предшествующем изложении предполагалось, что земля является гладкой сферой, окруженной однородной или простой атмосферой. Для таких условий расчет ожидаемой напряженности поля или потерь на передачу может быть выполнен с вполне удовлетворительной точностью для областей, находящихся в пределах прямой видимости или за пределами горизонта. Также может быть выполнена и интерполяция для промежуточных расстояний. Наличие холмов, зданий и деревьев сложным образом воздействует на распространение радиоволн, вследствие чего невозможно подсчитать ожидаемую в определенном пункте напряженность поля, если этот пункт расположен в непосредственной близости от подобных препятствий; невозможно даже определить средние значения напряженностей поля в пределах небольших площадок. Правда, обследовав профиль поверхности земли на пути распространения и введя определенные упрощающие допущения, можно вычислить средние значения поля, ожидаемые на площадках, представляющих собой как бы множество различных почв. [54]
Часть ее, определяющаяся возмущением атомных электронов, практически безынерционна и мгновенно следует за движением локализованного электрона. Иначе ведет себя доля поляризации, связанная с ориентацией существующих или индуцированных диполей. Так как перемещение ядер атомов и молекул происходит со скоростями, много меньшими скорости движения электрона, ориентационная поляризация обладает существенной инерционностью и не успевает следовать флуктуациям последнего. Раз возникнув, она в дальнейшем является энергетической ловушкой для электрона, ее образовавшего, даже в отсутствие каких-либо дефектов. Другими словами, локальная поляризация диэлектрика будет стационарно поддерживать электрон в локализованном состоянии, а он, в свою очередь, будет поддерживать стационарную поляризацию кристалла. Величина поляризации определяется квантово-механическим средним значением поля электрона и форму потенциальной ямы в этом случае можно рассчитать как потенциал системы идеальных диполей, размещенных в узлах кристаллической решетки. [55]
Предшествующее обсуждение основывалось на приближении, согласно которому ядро создает ди-польное поле. Это приближение было бы вполне правильным, если бы ядро имело исчезающе малые размеры или если бы электрон не мог приблизиться настолько близко к ядру, чтобы обнаружились конечные размеры последнего. На самом же деле ядро имеет конечные размеры ( его диаметр порядка 10 - 14 м), и, если электрон находится на s - орбитали, он может приблизиться к ядру вплотную. Будем считать, что электрон действительно проникает в ядро, и заменим ядерный магнитный момент эквивалентным круговым током с тем же радиусом, что и ядро. При сферическом распределении электрона за пределами кольцевого тока поле, действующее на электрон, усредняется и обращается в нуль, но внутри кольцевого тока поле имеет всюду одинаковое направление, никакой компенсации не происходит, и спиновый магнитный момент взаимодействует с ненулевым средним значением поля. Это взаимодействие изотропно, так как не зависит от ориентации остальной части ядерного остова молекулы. Оно характерно только для s - электронов, поскольку все другие орбитали имеют узел в ядре атома и не могут проникать в ядро. [56]
Страницы: 1 2 3 4