Зеемановское взаимодействие

Cтраница 1

Зеемановское взаимодействие, записанное в такой форме, соответствует частному случаю обобщенного вектора V, рассматриваемого в гл. [1]

Зеемановское взаимодействие электронных спинов здесь не учитывается. [2]

Если зеемановское взаимодействие намного больше спин-спинового, то его можно диагонализовать первым; для этого достаточно повернуть оси. [3]

Члены, учитывающие ядерное зеемановское взаимодействие, можно опустить, поскольку, как мы видели в гл. Большинство спектров свободных радикалов можно удовлетворительно объяснить в первом порядке теории возмущений. [4]

Квантование ядерного спина в суммарном поле Я и Не. [5]

Ясно, что ядерное зеемановское взаимодействие вызывает сдвиг линий поглощения. Более важно, однако, что оно приводит к появлению в спектре запрещенных переходов, при которых как электронный, так и ядерный спины изменяют направление на противоположное. [6]

Модуляция СТВ и зеемановского взаимодействия обусловлены внутрирадикальными процессами или процессами взаимодействия радикала с молекулами; они проявляются в спектрах разбавленных растворов радикалов. [7]

Первые два члена описывают зеемановское взаимодействие, третий - магнитную сверхтонкую структуру и последний - электрическое квадрупольное взаимодействие. Тот же самый гамильтониан используется для описания спектра иона, однако необходимо добавить члены, которые описывают взаимодействие иона с кристаллическим полем кубической симметрии. [8]

На этой основе результирующее ядерное зеемановское взаимодействие записывается в форме [ ср. [9]

Однако в твердых телах ядерное зеемановское взаимодействие может быть сильно изменено псевдоядерным зееманов-ским эффектом. Таким образом, значение gi часто невозможно определить с точностью, доступной методу тройного резонанса в атомных пучках, где поправки меньше и могут быть вычислены более точно. [10]

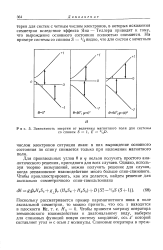Зависимость энергии от величины магнитного поля для системы со спином S 1, Е l / D. [11]

Чтобы привести матрицу оператора зеемановского взаимодействия к диагональному виду, выберем для спиновых функций новую систему координат, ось г которой составляет угол ю с осью г молекулы. [12]

Первая строка в (3.33) описывает зеемановское взаимодействие, вторая - то, что мы называем тонкой структурой резонансного спектра, а третья - сверхтонкое взаимодействие. В качестве приближений более высокого порядка можно еще учесть ядерное квадрупольное взаимодействие, которое оказывает влияние на энергетические состояния электронов через сверхтонкое взаимодействие. [13]

В статическом магнитном поле Я ядерное зеемановское взаимодействие приводит к расщеплению уровней на величину gi H. Для протонов в поле 100 кЭ это расщепление составляет около 400 МГц и равно kT, если Т - 0 02 К. Таким образом, для получения значительной ядерной поляризации требуются эти до некоторой степени экстремальные условия [29] и не удивительно, что этот метод поляризации ядер получил название метода грубой силы. Он соответствует достижению насыщения на кривой ядерной парамагнитной восприимчивости. Эффект аналогичен насыщению в электронном парамагнетизме, но так как для электронов g - 103 g /, то насыщение может быть легко достигнуто в поле 10 кЭ при температуре 1 К. [14]

В порошках двухквантовая прецессия благодаря зеемановскому взаимодействию приводит к спектрам в оя-области, что позволяет определить главные значения тензора химического сдвига. Обычные квадрупольные порошкообразные спектры появляются в о2 - области, и химическое экранирование и тензоры квадрупольного взаимодействия могут быть связаны друг с другом. В этом случае анизотропная часть зеемановского взаимодействия не появляется в двухквантовой оя-области. [15]

Страницы: 1 2 3 4