Ангармоничность

Cтраница 3

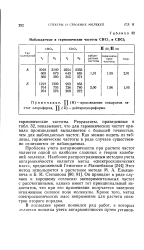Наблюдаемые и гармонические частоты СНС13 и CDC13. [31]

Проблема учета ангармоничности при расчете частот является одной из наиболее сложных в теории колебаний молекул. Он приводит в ряде случаев к хорошему согласию экспериментальных частот с рассчитанными, однако имеет тот принципиальный недостаток, что при его применении получается заведомо искаженное силовое поле молекулы. Кроме того, метод спектроскопических масс неприменим для расчета спектров второго порядка. [32]

Для учета ангармоничности необходимо добавить ряд членов ( сравн. [33]

Величину коэффициента ангармоничности и собственную частоту ( волновое число) колебаний определяют экспериментально по величинам частот ( волновых чисел) основной полосы поглощения, первого и второго обертона. [34]

Схема переходов и вид спектра для колебательно-вращательной полосы. Пунктиром показана пулевая линия, соответствующая чисто колебательному переходу. [35]

При учете ангармоничности в колебательных спектрах могут появляться обертоны основных частот колебаний ( Аи4; 1, напр. Важное значение, в частности для молекулярного спектрального анализа, имеет характеристичность в колебат. [36]

Классический учет ангармоничности в двухатомных молекулах приводит просто к небольшому изменению зависимости смещения от времени. Однако для многоатомных молекул изменение характера колебаний вследствие ангармоничности значительно более существенно, так как при наличии в выражении потенциальной функции членов, степень которых выше второй, уже нельзя провести строгое разделение колебательного движения на ряд простых движений ( нормальных колебаний), при которых все атомы двигаются вдоль прямых линий и имеют одинаковую частоту колебаний. Это легко представить себе совсем наглядно, если рассмотреть потенциальную поверхность фиг. В то время как для малых амплитуд два нормальных колебания v, и v, соответствуют простым колебаниям воображаемой точки вдоль прямой СС и вдоль прямой DD ( см. выше), для больших амплитуд подобное соответствие уже неприменимо. Если движение частицы начинается, например, из точки D, то ввиду отсутствия симметрии потенциальной поверхности по отношению к прямой DD оно будет происходить первоначально вдоль кривой DE ( линия наибольшего наклона в точке D) и затем выполнять сложные движения по фигурам Лиссажу, которые в принципе будут заполнять всю площадь потенциальной поверхности для энергий меньших, чем энергия в точке D. Если движение частицы начинается из точки С, то ввиду симметрии потенциальной поверхности по отношению к прямой СС она будет совершать простые колебания; однако при малейшем отклонении начальной точки от прямой СС снова возникает сложное движение по фигурам Лиссажу. [37]

Ввиду влияния ангармоничности вычисление постоянных наиболее общей квадратичной потенциальной функции заслуживает внимания только в том случае, если известны значения нулевых частот. Это имеет место только для молекул Нс 0 и D. [38]

Благодаря влиянию ангармоничности интервал между соседними колебательными уровнями уменьшается с увеличением общего числа квантов. Это приводит к уменьшению Z: для богатых энергией молекул, если эта энергия является колебательной. [39]

В случае электрической ангармоничности имеет место нелинейное изменение или дипольного момента ( инфракрасный спектр) или поляризуемости ( спектр комбинационного рассеяния) с расстоянием между ядрами. При точных расчетах интенсивностей и центров полос поглощения следует учитывать поправки на ангармоничность. [40]

Вычислить коэффициент ангармоничности молекулы С12, для которой известны собственная частота колебаний и энергия диссоциации. [41]

Существенного изменения ангармоничности VoH-колебаний при образовании водородной связи не происходит. Поэтому следует полагать, что спектроскопические массы водорода и дейтерия, хорошо компенсирующие ангармоничность колебаний свободной Н2О, окажутся эффективными и для связанных молекул воды. [42]

Кроме того, ангармоничность влияет на интенсивность колебательного ( инфракрасного) спектра молекулы, вызывая смешение полос, отвечающих колебаниям различной симметрии. В гармоническом приближении существует набор независимых колебательных движений молекулы, составляющих так называемые нормальные колебания. При наличии ангармоничности нормальные колебания уже не являются независимыми и энергия одного колебания может переходить к другим колебаниям. С позиций квантовой механики это можно объяснить смешением волновых функций колебаний различных типов, в результате которого смешиваются также характеристики различных нормальных колебаний. Важным примером ангармонического смешения нормальных колебаний является резонанс Ферми, обусловливающий одновременное возбуждение двух нормальных колебаний ( которое вызывает появление в спектре комбинационной полосы) при условии, что существует разрешенное нормальное колебание с частотой, близкой к частоте комбинационного перехода. [43]

Таким образом, электрическая ангармоничность может привести к изменениям интенсивности в колебательном спектре молекул, подобным изменениям, вызываемым механической ангармоничностью, но в отличие от последней электрическая ангармоничность не влияет на энергии самих уровней. [44]

Кроме того, кубичная ангармоничность [ слагаемое 8х3 в уравнении (10.2) ] вызывает изменение поляризуемости молекулы на основной частоте со. [45]

Страницы: 1 2 3 4