Вид - математическая модель
Cтраница 1
Вид математической модели зависит не только от свойств реального объекта, но и от требуемой точности. Любая математическая модель описывает реальный технологический объект с некоторой степенью приближения к действительности. [1]
Вид математической модели определяется теми упрощениями реальной физической картины процесса, которые допускаются при моделировании. Одним из самых распространенных, принятым в подавляющем большинстве случаев, является допущение об идеальном перемешивании жидкости - и идеальном вытеснении газа в пределах газожидкостного слоя на тарелках [309-316], причем во многих из упомянутых работ правомерность этих допущений подтверждена экспериментально. [2]
Вид математической модели и способ ее разработки выбирают на основании априорной информации об объекте моделирования ( сведений о природе объекта и степени его изученности) и целях использования моделей. [3]
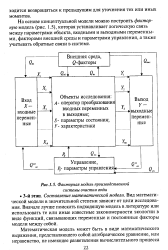 |
Факторная модель производственной системы очистки воды. [4] |
Вид математической модели в значительной степени зависит от цели исследования. [5]
Вид математической модели жидкостного экстрактора устанавливается в зависимости от внутренней структуры потоков, соответствующей заданному гидродинамическому режиму. Этот режим определяет основные параметры модели процесса, в том числе направление и скорости потоков в колонне, удерживающую способность, а также скорость масообмена через границу раздела фаз. [6]
Если выбор вида математической модели - это не формализуемая задача, то расчет параметров уже выбранной математической модели является чисто формальным процессом. [7]
Независимо от вида математической модели функционирования бывают детерминированными или стохастическими с непрерывными или дискретными параметрами. Для детерминированной модели предполагают, что все параметры известны и соотношения между ними остаются вполне определенными. При этом для одного и того же комплекса параметров при каждом последующем расчете получают один и тот же результат. Для стохастической модели приходится учитывать различные случайные факторы и располагать экспериментальными данными обо всех параметрах в результате измерений. Сбор массовой информации о параметрах затруднителен, а уменьшение объема информации нежелательно, так как это приводит к получению менее надежных результатов. Затраты времени на сбор и обработку статистической информации значительно сокращает применение ЭВМ. [8]
В зависимости от вида математических моделей, используемых для описания потоков событий, и сложности изучаемой системы вероятностные характеристики последней могут быть получены аналитически или методом моделирования. При этом в первом случае обычно используются гипотезы о потоках и их свойствах, во втором - экспериментальные распределения. Заметим, что лишь для некоторых частных случаев ПС вероятностные характеристики, например, уровней запасов, моментов и размеров отказов ( дефицита) в обслуживании могут быть получены теоретически. Теоретические результаты, определяющие, например, закон переключения интенсивности обслуживания, а также момент, когда такое переключение целесообразно, относятся в основном к случаям, когда система описывается управляемым марковским процессом и оптимальные стратегии находятся в классе марковских. Для таких систем, в зависимости от числа требований в системе, удается выбрать уровень переключения скорости работы и устанавливать среднюю длительность обслуживания, минимизирующую критерий, учитывающий средние потери, вызванные задержками в обслуживании, и затраты от обслуживания с той или иной интенсивностью работы. Однако эффективность функционирования такого алгоритма управления в условиях реальных ПС существенно зависит от того, насколько реальные потоки требований близки к простейшему потоку. [9]
Рассмотрим только некоторые вида математических моделей, описывающих динамику тарельчатых ректификационных колонн. [10]
Каждая из этих видов математических моделей может предназначаться для рассмотрения течений различного вида: стоковых, сейшевых, ветровых или суммарных. [11]
Каждая из этих видов математических моделей может предназначаться для рассмотрения течений различного вида: стоковых, сейшевых, ветровых или суммарных. [12]
В зависимости от вида математической модели технического объекта критерии могут быть детерминированные или статистические. [13]
Метод решения определяется видом математической модели. В данном случае задача оптимального календарного планирования сформулирована как многомерная задача о ранце с дополнительными блочными ограничениями - равенствами. [14]
В соответствии с видом математической модели объекта управления, их математические модели и задачи управления делятся на статические и динами-неские. [15]
Страницы: 1 2 3 4