Частичная сумма - ряд
Cтраница 1
Частичные суммы рядов Фурье для тех или иных функций часто называют суммами Фурье этих функций. [1]
Частичные суммы рядов Фурье являются непрерывными функциями. Поэтому, согласно § 4 главы 5, сходимость ряда Фурье какой-либо функции в точке ее разрыва не может быть равномерной. Для выяснения поведения рядов Фурье в точках разрыва соответствующих функций рассмотрим некоторые общие черты неравномерной сходимости непрерывных функций. [2]
Частичные суммы ряда ( 1) являются многочленами. [3]
Поэтому частичные суммы ряда (4.32) с четными номерами составляют ограниченную последовательность. [4]
Вычислим отдельно частичные суммы ряда ( 5) с четным и нечетным числом слагаемых. [5]
 |
Иллюстрация метода Ньютона.| Алгоритм метода Ньютона. [6] |
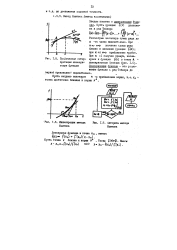
Рассмотрим частичную сумму ряда до К - го члена включительно. При К % оо значение суммы ряда близко к значению функции f ( х); при к оо приближение грубое. При к 1 получим прямую, касаю - 1.5. Графическая интер - щуюся к функции f ( x) в точке А. [7]
Рассмотрим частичную сумму ряда до К - го члена включительно. При Кв о значение суммы ряда близко к значению функции f ( х); при к оо приближение грубое. [9]
Если последовательность частичных сумм ряда с неотрицательными членами ограничена, то ряд сходится. [10]
Если последовательность частичных сумм ряда (35.1) сходится, то он называется сходящимся рядом, а если она расходится, то расходящимся. [11]
Последовательность графиков частичных сумм ряда Фурье кусочно-гладкой функции сходится ( равномерно. [12]
Если последовательность частичных сумм ряда сходится, то ряд называется сходящимся, а предел частичных сумм называется суммой ряда. [13]
Если последовательность частичных сумм ряда а неотрицательными членами ограничена, то ряд сходится; Если последовательность частичных сумм ряда с неотрицательными членами неограничена, то ряд расходится к оо. [14]
Для последовательностей частичных сумм ряда Тэйлора такой выбор может быть эффективно проведен следующим путем. [15]
Страницы: 1 2 3 4