Адекватность - математическая модель
Cтраница 1
Адекватность математической модели устанавливается методами математической статистики. [1]
Адекватность математической модели - свойство правильно отражать реальные процессы, протекающие в синтезируемом объекте. [2]
Адекватность математической модели особенно важна в задачах эксплуатации, где непосредственно можно сопоставлять расчетные и фактические значения параметров и проверять правильность модели. При оптимизации режимов эксплуатирующихся газовых систем используются уравнения течения в трубах и формулы для расчета нагнетателей и КС, о которых шла речь в гл. По многим причинам теоретические значения некоторых коэффициентов в этих соотношениях существенно отличаются от фактических. Точнее, теоретическая модель оказывается недостаточно хорошей для описания реального объекта. [3]
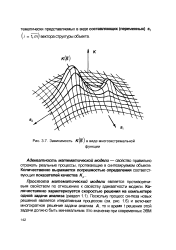 |
Зависимость K ( S в виде многоэкстремальной. [4] |
Адекватность математической модели - свойство правильно отражать реальные процессы, протекающие в синтезируемом объекте. [5]
 |
Схема поташной очистки конвертированного газа от двуокиси углерода. [6] |
Адекватность математической модели реальному процессу проверялась сравнением рассчитанных по модели и определенных экспериментально - профилей изменения концентрации двуокоси углерода и концентрации карбоната и бикарбоната калия в насыщенном растворе поташа по высоте абсорбера. [7]
Адекватность математической модели - это соответствие модели моделируемой задаче или процессу принятия решений, причем адекватность рассматривают по тем свойствам модели, которые для ЛПР являются наиболее важными в данный момент времени. Математическая модель называется адекватной по вектору Y, если погрешность расчета на ее основе значений выходных параметров yi e У не превышает заданных. Как известно, адекватность математической модели обычно рассматривают в ограниченной области изменения входных переменных. Эту область называют областью адекватности математической модели. [8]
Адекватность математической модели проверяется при помощи / - критерия Фишера. [9]
Адекватность математической модели, входящей в моделирующий блок, проверена с использованием обратноосмотичес-кой установки с аппаратом, имевшим два последовательн. [10]
Адекватность математической модели процесса ректификации нефтяных смесей реальному процессу обеспечивается за счет использования надежных аналитических зависимостей для расчета физико-химических и термодинамических свойств углеводородов и узких нефтяных фракций, а также корректности решения системы нелинейных уравнений, описывающих процесс ректификации нефтяных смесей в сложных разделительных системах. [11]
Здесь адекватность математической модели реальной ситуации определяется физической моделью задачи, так как последняя однозначно определяет МПЗ. [12]
От адекватности математических моделей энергетических характеристик гидроагрегата натурному объекту во многом зависит и эффективность работы ГЭС в целом. Особенно это относится к плотинным схемам ГЭС, где потери мощности в агрегате составляют значительную долю ДЛтэс. [13]
Установление адекватности математической модели реальному объекту осуществляется путем непосредственного сравнения ( в смысле принятого критерия) выходных величин этого объекта с выходными величинами модели. Если модель объекта управления представляется системой дифференциальных уравнений, то указанное сопоставление выходных величин, естественно, требует предварительного решения дифференциальных уравнений при определенных начальных и граничных условиях, аналогичных условиям протекания реального процесса в аппарате. В связи с этим унификация математических моделей приводит соответственно и к унификации методов решения дифференциальных уравнений, которыми описываются процессы в аппаратах. Поэтому стремление к унификации моделей и методов их математического исследования оправдано, если при этом ставится задача совмещения модели с реальным объектом, например варьированием входящими в математическую модель коэффициентами. [14]
Проверка адекватности математической модели показала, что расхождение расчетных и экспериментальных данных находится в пределах доверительного интервала. [15]
Страницы: 1 2 3 4