Адекватность - математическая модель
Cтраница 3
Для проверки адекватности математической модели реальному процессу необходимо сравнить результаты измерения на процессе с результатами предсказания модели в идентичных условиях. Поэтому всегда желательно, перед тем как приступить к решению оптимальной задачи, удостовериться в адекватности имеющейся модели. [31]
 |
Зависимость осе вого усилия сжатия от перемещения торца сильфоиа. [32] |
Следует подчеркнуть высокую адекватность математической модели реальной работе КЭ. [33]
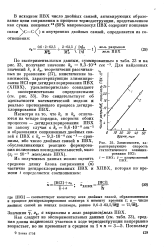 |
Зависимости, характеризующие скорость статистического элиминирования НС1. [34] |
Это свидетельствует об адекватности математической модели и реально протекающего процесса дегидро-хлорирования ПВХ. [35]
Задачи определения областей адекватности математических моделей отличаются от задач назначения допусков при заданном векторе поминальных значений тем, что вписывание производится не в пространстве параметров элементов, а в пространстве внешних параметров, так как область адекватности должна характеризовать диапазоны изменения внешних переменных, в которых математическая модель адекватна. [36]
Рассмотрим алгоритм оценки адекватности математической модели функции отклика на ином принципе априорного формирования альтернативных классов эквивалентности. [37]
Вычислительные эксперименты по оценке адекватности математических моделей и алгоритмов подразумевают их планирование, ориентирующееся на обеспечение наиболее точной или приемлемой оценки уровня адекватности при условии минимизации затрат на исследование этой адекватности или невыхода уровня таких затрат за установленное заранее значение. [38]
Однако, стремясь к повышению адекватности математических моделей, необходимо помнить об исключительно большой трудоемкости кинетических расчетов деформирования конструкции. Некоторые возможности ее уменьшения иллюстрирует вторая половина данной книги. Однако здесь несомненно существуют дополнительные резервы, которые состоят в рациональном использовании современных ЭВМ. В частности, имеется в виду составление пакетов прикладных программ, достаточно универсальных и гибких для их постоянного совершенствования по мере накопления экспериментальных данных и опыта расчетов. Для выполнения вариантных расчетов конструкций могут оказаться удобными программы для миникомпьютеров, ориентированные на определенные типы конструктивных элементов и конкретные материалы и использующие данные предварительных расчетов, в более простых случаях - номограммы. [39]
Одной из проблем является проверка адекватности математической модели физическому явлению, которая включает в себя доказательство теорем существования, единственности и устойчивости решения. Такой анализ часто затруднителен в силу нелинейности, вырождения и сложности структуры уравнений и краевых условий, составляющих математическую модель. Достаточно сложным в плане обоснования и практической реализации является численное решение математических задач. Наконец, всегда желательно проведение физического эксперимента, подтверждающего или опровергающего математическую теорию. При выполнении эксперимента возникают трудности, связанные с методикой проведения эксперимента, погрешностями измерений и учетом влияния посторонних факторов. [40]
При каких условиях не соблюдается требование адекватности математической модели и как следует поступить в этом случае. [41]
Очевидно, предлагаемая формализация сопряжения агрегатов обеспечивает адекватность математической модели и реальной системы лишь при условии, что структура наборов входных, управляющих и выходных контактов агрегатов соответствует структуре сигналов, рассматриваемых как конечные совокупности одновременно поступающих элементарных сигналов. [42]
Несмотря на необходимость индивидуального обсуждения и оценки адекватности математической модели, как правило, в каждом конкретном случае следует отметить несколько общих принципиальных моментов и общепринятых допущений. [43]
Этот прием является основным при установлении соответствия адекватности математической модели изучаемому объекту. Поэтому прежде всего необходимо рассмотреть методы математической оценки различных сигналов и кривых отклика системы на подаваемое возмущение. [44]
Анализ эффективности решающей функции в задаче оценки адекватности математической модели функции отклика сводится к анализу оперативной характеристики. В свою очередь значения оперативной характеристики определяются, как это следует из выражений (8.63) и (8.67), значениями функций нецентрального - распределения с vn - / ст. св. De известно, и значениями функции нецентрального распределения Фишера с п - I и v2N - n ст. св. Конечных выражений таких нецентральных распределений не существует, также как не существует и табулированных значений. Поэтому проблема вычисления значений функций нецентральных распределений может быть решена либо путем создания соответствующих программных пакетов и использования компьютера, либо путем аппроксимации нецентральных распределений центральными, для которых существуют табулированные значения. Рассмотрим второй путь сначала для нецентрального - распределения с vn - / ст. св. [45]
Страницы: 1 2 3 4