Пространственное возмущение
Cтраница 1
Рассмотрение пространственных возмущений показывает, что в случае поперечной вибрации при всех Рг плоские возмущения наиболее опасны. [1]
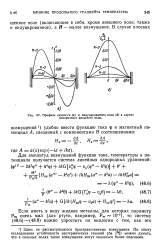 |
Профиль скорости ( а и индуцированное поле ( б в случае. [2] |
Здесь не рассматриваются пространственные возмущения. [3]
Что же касается пространственных возмущений, для которых k Ф 0 и &2 Ф О, то расчет, проведенный Чандрасека-ром, показал, что они приводят к более высоким критическим числам Рэлея. [4]
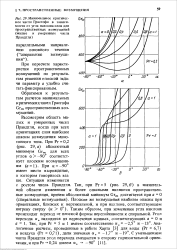 |
Минимальное критическое число Грасгофа в зависимости от угла наклона слоя для пространственных возмущений ( малые и умеренные числа Прандтля. [5] |
При пересчете характеристик пространственных возмущений по результатам решения плоской задачи параметр а удобно считать фиксированным. [6]
В этом параграфе мы рассмотрим пространственные возмущения стационарного конвективного движения в плоском наклонном слое. [7]
 |
Критическое число Грасгофа в зависимости от числа Прандтля. а На поперечное поле. б На 20, продольное поле. [8] |
Таким образом, критическое число Gr для пространственных возмущений с волновыми числами ky и kz в поле На определяется через критическое число Gr для плоских возмущений с волновым числом JF в поле На. Преобразования (17.10) аналогичны известным преобразованиям Хан-та [7] в теории устойчивости плоскопараллельных изотермических течений. [9]
Описанный выше метод вычисления производных неприменим для некоторых типов пространственных возмущений системы. В работе В. Г. Золотухина и др. ( 1968) разработаны эффективные алгоритмы метода Монте-Карло для расчетов билинейных функционалов, входящих в формулу теории малых возмущений. Однако этот метод также не является универсальным. Автором настоящей монографии предложен простой по идее, трудоемкий, но универсальный способ реализации формул теории возмущений. Он основан на моделировании траекторий дополнительных частиц для статистической оценки функции ценности. В целях упрощения излагаемого материала этот способ приведен для случая малых возмущений. [10]
Таким образом, в случае горизонтального слоя критические числа Грасгофа для плоских и пространственных возмущений совпадают. Задача для амплитуд пространственных возмущений (7.2) - (7.7) при а - 90 не содержит - отдельно волновых чисел ky и kz, а. Декременты возмущений X и критические числа Грасгофа Gr поэтому не зависят от направления волнового вектора k ( ky, kz), а определяются лишь его величиной. [11]
Нет необходимости приводить здесь уравнения малых возмущений и спектральные амплитудные задачи для плоских и пространственных возмущений конвективного течения в наклонном слое - они по виду совпадают с соответствующими задачами, приведенными в § 6 и 7, разумеется, с надлежащей заменой профилей скорости и температуры основного течения и с введенным в предыдущем параграфе определением числа Грасгофа. [12]
Для исследования радиальной однородности вещества выполнено моделирование одномерного взрыва цилиндрической проволочки в предположении малости пространственных возмущений формы и равенства электронных и ионных температур. [13]
Только при малых Le в узком диапазоне изменения параметра z граница устойчивости может определяться развитием пространственных возмущений. [14]
В теории устойчивости плоскопараллельных изотермических течений существует известное преобразование Сквайра [27 6], сводящее задачу об устойчивости относительно пространственных возмущений к соответствующей задаче для плоских возмущений. Полученные Сквайром формулы преобразования числа Рейнольдса и волнового числа позволяют получить всю информацию об устойчивости из решения двумерной краевой задачи Орра - Зоммерфельда. При этом оказывается, что плоские возмущения более опасны: им соответствуют наименьшие критические числа Рейнольдса. [15]
Страницы: 1 2 3 4