Пространственное возмущение

Cтраница 2

В обсуждаемой проблеме из-за наличия продольного градиента температуры не удается получить преобразования, сводящие задачу о пространственных возмущениях к соответствующей плоской задаче. Поэтому далее будут рассмотрены два предельных случая - плоские возмущения в виде валов с осями, перпендикулярными направлению основного потока, и пространственные спиральные возмущения в виде валов с осями, параллельными основному потоку. [16]

Последний член в уравнении ( 16), очевидно, характеризует отклонение от равновесного потока, обусловленное временной релаксацией пространственных возмущений. [17]

Как и в случае конвективного течения вязкой жидкости в вертикальном слое ( см. § 7), можно показать, что пространственные возмущения менее опасны, чем плоские. [18]

Частотно-избирательные ответвители для использования в волоконно-оптической связи. [19]

Направленная связь между двумя различными волноводами может быть сделана частотно-избирательной и весьма эффективной при условии, что достигнута синхронизация фаз с помощью периодичег ского пространственного возмущения показателя преломления. При этом в зависимости от периода решетки могут быть реализованы как попутная, так и встречная связи. Согласно условию (11.8.30), для попутной связи на длине волны XQ требуется решетка с периодом Л / ( па - пь), в то время как для встречной связи на такой же длине волны период решетки должен быть равен Л / ( па /), где пи, п, - эффективные показатели преломления для мод волноводов а и Ь соответственно. Однако такой ответвитель труднее изготовить, так как для этого нужно иметь решетки с очень небольшим периодом. На рис. 11.26 показан схематически ответвитель на встречной связи для применения в волоконно-оптических линиях связи. [20]

Существенно, что кривая 2 не является границей устойчивости к одномерным ( К2: 0) возмущениям, а определяет предельное положение границы устойчивости по отношению к пространственным возмущениям при К2 - О, когда возмущение принципиально является двумерным. [21]

В выражении ( 7) З У, в и 8t / 1 представляют собой соответственно пространственное и временное возмущения потока в бесфлуктуационно-безъемкостной системе; S / j - пространственное возмущение потока в флуктуационно-безъемкостной системе; а 8т / 1 - временное возмущение потока в бесфлуктуационно-емкостной системе. [22]

В самом деле-любое малое пространственное возмущение в линейном случае можно представить в виде суперпозиции плоских волн, для каждой из которых решение уже найдено. [23]

Таким образом, в случае горизонтального слоя критические числа Грасгофа для плоских и пространственных возмущений совпадают. Задача для амплитуд пространственных возмущений (7.2) - (7.7) при а - 90 не содержит - отдельно волновых чисел ky и kz, а. Декременты возмущений X и критические числа Грасгофа Gr поэтому не зависят от направления волнового вектора k ( ky, kz), а определяются лишь его величиной. [24]

В настоящее время хорошо развиты численные методы решения в основном одномерных нестационарных задач. Большой интерес вызывает также поведение пространственных возмущений, для анализа которого необходимо решение двух - и трехмерных нестационарных задач с произвольными несимметричными начальными условиями. Однако такие задачи до сих пор трудны для численного интегрирования. [25]

Потенциально неустойчивая стратификация делает необходимым исследование пространственных возмущений. Зависимость формы профиля основного течения от Ra и наличие в уравнении переноса тепла дополнительного члена, учитывающего продольный градиент, делают невозможным сведение пространственной задачи к плоской. Между тем есть основания думать, что, как и в случае наклонного слоя, при определенных условиях ( преобладающая роль стратификационного механизма неустойчивости) пространственные возмущения могут стать наиболее опасными. Как можно видеть из уравнений (8.8), такие возмущения не взаимодействуют с основным потоком. Амплитудная задача не содержит скорости и температуры основного течения. [26]

Изложенные в § 4 и 6 результаты дают ответ на вопрос о структуре спектра возмущений и границах устойчивости конвективного течения в вертикальном и наклонном слоях жидкости относительно плоских возмущений. В этом параграфе будет рассмотрен вопрос о поведении пространственных возмущений. [27]

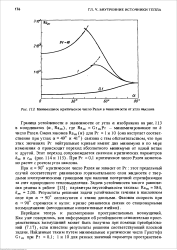Минимальное критическое число Рэлея в зависимости от угла наклона. [28]

Как уже говорилось, вся информация об устойчивости относительно пространственных возмущений может быть получена при помощи преобразований (7.17), если известны результаты решения соответствующей плоской задачи. [29]

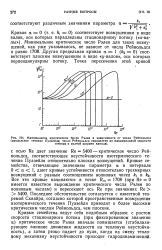Минимальное критическое число Рэлея в зависимости от числа Рейнольдса ( продольное течение Пуазейля. число Рейнольдса определено по максимальной скорости. [30]

Страницы: 1 2 3 4