Малое случайное возмущение

Cтраница 1

Малые случайные возмущения могут принимать большие значения, но вероятность этих больших значений мала. Во-вторых, рассмотрение в качестве возмущений случайных процессов расширяет понятие стационарности возмущений. [1]

Схема нагружения колес. 1 - ведущего. 2 - ведомого. [2]

Если под воздействием малого случайного возмущения деформация в некоторый момент времени t 0 увеличилась на величину Л60, то возрастает и усилие на зуб, условия равновесия колес при постоянных значениях моментов 7 и 72 нарушатся, и угловые скорости колес начнут периодически изменяться, что будет сопровождаться изменением усилия и деформации с той же частотой. [3]

Совместное движение упругих зубьев вдоль линии зацепления С, Сг. 1 2 - положение соприкасающихся поверхностей зубьев в момент времени t. Г, 2 - положение в момент времени ( dt ( вся дефор. мация зубьев условно показана в виде деформации смятия. [4]

Если под воздействием малого случайного возмущения деформация в некоторый момент времени г О увеличилась на величину Дбд, то возрастает н усилие на зуб, условия равновесия колес при постоянных значениях моментов М - н A / j нарушатся, и угловые скорости колес начнут периодически изменяться, что будет сопровождаться изменением усилия и деформации с той же частотой. [5]

Посмотрим, какие могут быть модели малых случайных возмущений, и какие задачи естественно для них рассматривать. [6]

Общее правило для обращения с системами уравнений, включающими малые случайные возмущения, состоит в том, чтобы решить систему с точностью до членов второго порядка по возмущениям. [7]

Изложенный способ определения собственной частоты и формы колебаний при наличии малых случайных возмущений параметров позволяет определить математическое ожидание и дисперсию X, и Ws ( I) исходной гйросистемы. [8]

Одной из наиболее интересных задач такого рода является задача о малых случайных возмущениях периодических режимов в системах с нелинейностями релейного типа. [9]

Таким образом, можно предположить, что при воздействии на пламя малых случайных возмущений возникает турбулентный режим течения и горения. [10]

В главе 8 содержатся применения полученных в предыдущих главах результатов к исследованию устойчивости относительно малых случайных возмущений. Мы вводим некоторую числовую характеристику устойчивости, которая связана с функционалом действия. Рассматривается ряд задач оптимальной стабилизации. [11]

В главе 10 речь идет о некоторых вопросах нейтронной и зарядовой кинетики, включая стохастические задачи при наличии малых случайных возмущений и диффузию нейтронов в тороидальном ядерном электрогенераторе. В главах 11 и 12 предложены стабилизационные и фильтрационные схемы решения задач управляемой адаптивной ядерной кинетики. [12]

Для маловязких ЖВВ критическое давление р %, при котором наступает автотурбулизация горения в условиях экспериментов при постоянном давлении, когда имеются конечные возмущения, вызванные процессом воспламенения, мало отличается ( на 20 - 30 %) от критического давления ркр, полученного в условиях горения в манометрической бомбе, когда имеются лишь бесконечно малые случайные возмущения. Этот результат показывает, что условия устойчивости горения маловязких жидкостей практически одинаковы для бесконечно малых и конечных возмущений. Следовательно, выводы теории, полученные для бесконечно малых возмущений, пригодны для оценки устойчивости горения к конечным возмущениям. [13]

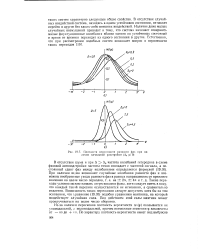Плотности вероятности разности фаз при наличии начальной расстройки ( Д0 - ф. 0. [14]

В отсутствие случайных воздействий система, находясь в одном устойчивом состоянии, не может перейти в другое без каких-либо внешних воздействий. Наличие даже малых случайных возмущений приводит к тому, что система начинает совершать малые флуктуационные колебания вблизи одного из устойчивых состояний и время от времени переходит из одного состояния в другое. [15]

Страницы: 1 2