Волна - изгиб
Cтраница 1
Волна изгиба распространяется с переменной скоростью. [1]
Скорости волн изгиба и возмущения совпадут, что приведет к резкому увеличению амплитуды волн в шине. Это в свою очередь может привести к разрыву шины. [2]
Скорости волн изгиба и возмущения совпадут, что приводит к резкому увеличению амплитуды волн. Это в свою очередь может привести к разрыву шины. [3]
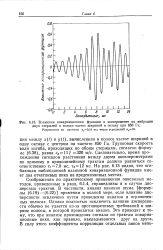 |
Взаимная ковариационная функция в эксперименте по вибрации двух стержней в полосе частот шириной в октаву при 850 Гц. Разрешение по времени те0 10 мс. число усреднений п - 15. [4] |
Групповая скорость волн изгиба, проходящих по обоим стержням, согласно формуле (6.38), равна cg-llf 320 м / с. Следовательно, время прохождения сигналом расстояния между двумя акселерометрами во прямому и криволинейному трактам должно равняться соответственно Ti 7 8 мс, t212 мс. На рис. 6.13 видно, что огибающая наблюдаемой взаимной ковариационной функции имеет два отчетливых пика на предсказанных местах. [5]
Зато скорость волн изгиба, образующихся в плоских плитных элементах, зависит от частоты и, кроме того, от поперечного сечения этого элемента. В принципе волны изгиба в элементах большей толщины распространяются с большей скоростью, чем в тонких элементах. К тому же волны изгиба более высоких частот распространяются скорее, чем низких частот. Эта зависимость показана на рис. 10, заимствованном из работ Гезеле. [6]
Общее выражение для распространения волны изгиба вдоль s есть периодическая функция s - Vt, где V скорость распространения волны. [7]
При увеличении начальной длины волны изгиба трубопровода и различных значениях о кривые асимптотически приближаются к значению критического усилия, соответствующего неискривленному трубопроводу. Это наблюдается и при уменьшении параметра начальной стрелки прогиба при постоянной длине волны изгиба. [8]
Аналогичные результаты справедливы и для волн изгиба тонких стержней; колебания изгиба предполагаются малыми. [9]
Очевидно, что при формировании волны изгиба в плоской форме, в отличие от предыдущих случаев, сечения сохранят ориентацию и относительно оси скважины. [10]
Аналогичные результаты справедливы и для волн изгиба тонких стержней; колебания изгиба предполагаются малыми. [11]
В том случае, если длина волн изгиба соизмерима с размерами поперечного сечения стержня, для определения собственных частот поперечных колебаний стержней следует учитывать инерцию поворота сечения и действие перерезывающих сил. [12]
Измерения с помощью продольных воли и волн изгиба в тонких полосках могут охватывать диапазон частот от 100 до 40 000 гц, при этом имеется, возможность непрерывного изменения частоты. При значительно более высоких частотах, когда длина волны слишком мала, чтобы ее можно было точно измерить, и поперечные размеры образца сравнимы с длиной волны, сведения о динамических свойствах при сдвиге можно получить, проследив распространение поперечных волн другим способом. Измеряется время прохождения импульса волн сдвига через образец известной толщины и уменьшение его амплитуды при прохождении. [13]
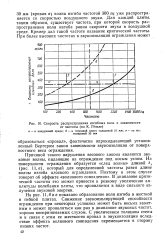 |
Скорость распространения изгибных волн в зависимости от частоты ( по К - Гезеле. [14] |
На рис. 11 бив показано образование волн изгиба в жесткой и гибкой плитах. Снижение звукоизолирующей способности ограждения при некоторых условиях может быть весьма заметным и может проявляться как раз в диапазоне звуковых частот, хорошо воспринимаемых слухом. С увеличением толщины стены и в связи с этим ее жесткости провал в звукоизоляции вследствие эффекта волнового совпадения перемещается в сторону низких частот. [15]
Страницы: 1 2 3 4