Неэволюционная ударная волна

Cтраница 2

Наглядно можно представить, что в пределе при R - оо или Eq. Структуры неэволюционных ударных волн, возникающих при переходе к МГД-пределу, оказываются неоднозначными, их вид зависит от предельного перехода. [16]

Вообще говоря, не очевидно, что все эволюционные волны имеют структуру. Заметим, что в случае медленных ударных волн существование структуры доказано лишь для волн малой, но конечной интенсивности. В случае неэволюционных ударных волн всегда можно подобрать диссипативные коэффициенты так, что решение, представляющее структуру, отсутствует. [17]

Области, соответствующие эволюционным ударным волнам, затенены. Интервал BCD на кривой Гюгонио соответствует неэволюционным ударным волнам. Волны, принадлежащие сегментам адиабаты Гюгонио, которые лежат в прямоугольниках выше биссектрисы, проходящей через точки A, D и F, не могут иметь структуры, так как они соответствуют ударным волнам разрежения и не удовлетворяют энтропийному условию. Интервал BCD кривой Гюгонио неэволюционен по отношению к вращательным ( выходящим из исходной плоскости) возмущениям. Структура ударных волн, принадлежащих сегменту ВС ударной адиабаты, неединственна. [18]

Если направления B L и B R образуют угол, отличающийся от 180 на 10 или более градусов, то, хотя все возможные ударные волны имеют коллинеарные В и BR, образуется расширяющаяся со временем волна, в которой сосредоточено все вращение вектора Вт. Значение Iz увеличивается со временем, и эта волна в конце концов становится вращательной. На начальных стадиях своей эволюции эта волна близка к неэволюционным ударным волнам 1 - 3 или 2 - 3, а ее ширина значительно больше ширины альфвеновского разрыва, если бы такой образовался одновременно с ней. [19]

При очень больших магнитных числах Рейнольдса такая волна должна быстро распасться под действием альфвеновских возмущений и не должна реализоваться в физических процессах. Как упоминалось ранее, особенность магнитной газовой динамики заключается в том, что существуют разрывы, которые неэволюци-онны только по отношению к альфвеновским ( вращательным) возмущениям. Поэтому, если рассматривается строго компланарная задача ( векторы скорости и магнитного поля лежат в одной плоскости с вектором нормали к разрыву, и система уравнений включает в себя только две компоненты векторов), построение решения возможно как с помощью эволюционных, так и с помощью неэволюционных ударных волн, которые, однако, эволюционны при строгой компланарности. В зависимости от использованного метода неэволюционное решение в виде составной волны может реализоваться в вычислениях, так как в фазовом пространстве оно лежит ближе к начальным условиям. Если решается полная система МГД-уравнений с тремя компонентами векторов скорости и магнитного поля и небольшое поперечное возмущение добавляется к вектору магнитного поля, при достаточно больших временах составная волна распадается на вращательный разрыв и медленную ударную волну. [20]

Интегральные кривые упрощенной МГД-системы. [21]

Заключенные в скобки числа 1, 2 и 3 обозначают типы состояний перед или за разрывом. Существует скорость ударной волны, соответствующая касательной к графику функции аВу, проведенной из точки ( By, a ( By) 3) ( см. рис. 5.18 Ь), когда возможные состояния типов 1 или 2 перед разрывом сливаются. Неэволюционная ударная волна 2 - ) 3 имеет структуру, представленную одной из двух симметричных интегральных кривых. Неэволюционной ударной волне 1 - 3 может быть приписано однопараметрическое непрерывное множество интегральных кривых, соответствующих различным структурам этого разрыва. [22]

Трехмерная форма головной ударной волны. [23]

Здесь В - точка, в которой внешнее магнитное поле нормально к поверхности ударной волны. Сегменты АВ, ВС и CD являются, соответственно, быстрой, 1 - 3 трансальфвеновской и опять быстрой ударными волнами. На сегменте СЕ ударная волна изменяет тип от 2 - 4 трансальфвеновского до медленного. Из рисунка видно, что различные типы неэволюционных ударных волн кажутся неизбежными. Причиной такого утверждения может быть тот факт, что всегда можно выбрать плоскость, в которой будут лежать как вектор скорости, так и вектор напряженности магнитного поля, и эта плоскость окажется новой плоскостью симметрии задачи. При этом ясно, что для разрушения неэволюционного решения, необходимо возмущать плоскость симметрии. Это подразумевает, что если ожидается присутствие неэволюционных ударных волн, обусловленное симметрией задачи, то ее нужно решать, пренебрегая присутствием этой плоскости и вводя возмущения, выводящие BOO и VQO из нее. Приведенные здесь рассуждения в равной мере относятся и к случаю СВ-ЛМС взаимодействия в диапазоне неэволюционности отдельных сегментов головной ударной волны. [24]

По сравнению с рассмотренным выше случаем аА се роль волны 1 - 3 играет теперь волна 2 - 4, в то время как ударная волна 2 - 3 сохраняет свои свойства. Численные эксперименты, проведенные в вышеупомянутых работах, имели дело с откликом стационарных структур неэволюционных ударных волн типа 2 - 3 и 2 - 4 на альфвеновские возмущения, приходящие к ним с передней стороны. [25]

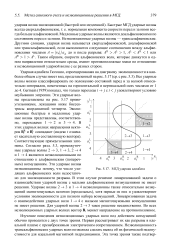МГД ударная адиабата. [26]

Медленные ударные волны являются доальфвеновскими по состояниям перед и за ними. Неэволюционные ударные волны - трансальфвеновские. Другими словами, ударная волна называется сверхальфвеновской, доальфвеновской или трансальфвеновской, если выполняются следующие соотношения между альфве-новскими числами А vn / aA до и после разрыва: AR AL 1, AL AR 1 или AR 1 AL. Таким образом, скорости альфвеновских волн, которые движутся в одном направлении относительно среды, имеют противоположные знаки по отношению к неэволюционной ударной волне с ее разных сторон. [27]

Путем численного эксперимента было показано, что структуры неэволюционных ударных волн могут быть довольно устойчивыми к расщеплению под действием альфвеновских возмущений. Они могут поглощать эти возмущения, меняя или свою внутреннюю структуру, если она описывается свободным параметром, или интенсивность. Неэволюционная ударная волна может также расщепиться на эволюционную ударную волну и неэволюционную волну другого типа. Количество альфвеновских возмущений, необходимых чтобы это произошло, зависит от величины диссипативных коэффициентов, определяющих толщину структуры, а следовательно, от возможности неэволюционной ударной волны абсорбировать приходящие возмущения. В пределе исчезающей диссипации достаточно бесконечно малого альфвеновского возмущения, для того чтобы сделать неэволюционный разрыв неотличимым от вращательного. В этом смысле полученные в вышеупомянутых работах результаты не противоречат классическим результатам, относящимся к идеальной магнитной газовой динамике. Исключение могли бы составить такие случаи, в которых, по мере того как диссипативные коэффициенты стремятся к нулю, все более и более жесткие ограничения накладываются на малость приходящих альфвеновских возмущений. [28]

Другая серия численных экспериментов ( Markovskii, Skorohodov, 2000b) относится к отклику неэволюционных ударных волн на резкое изменение диссипативных коэффициентов среды. Здесь v - это некоторый обобщенный диссипатив-ный коэффициент, определяющий ширину структуры ударной волны. При изменении v точка, представляющая неэволюционную ударную волну в плоскости ( q, v - llz), изменяет свою ординату. В результате, распад начальной волны происходит в соответствии со сценарием, описанным ранее. [30]

Страницы: 1 2 3