Нерегулярная волна
Cтраница 1
Динамическое воздействие нерегулярной волны на сквозное сооружение, расположенное в глубоководной зоне моря. [1]
В случае воздействия нерегулярных волн число шагов интегрирования по высоте существенно влияет на затраты машинного времени, так как на каждом уровне по высоте и на каждом шаге Дг выполняется численный счет скоростей и ускорений по большому числу JVE гармоник ( см. разд. Вычисления показали, что при сохранении указанного разбиения участка ( Я, z, ( t)) оптимально разбиение постоянного интервала с шагом 0 1 Я. [2]
При изучении процесса воздействия нерегулярных волн на сооружения последнее можно рассматривать как линейную динамическую систему, на вход которой поступает случайный стационарный процесс - волнение. Тогда деформация сооружения является выходом данной системы и также представляет случайный стационарный процесс. Для случайных стационарных процессов известна методика определения энергетических спектров с помощью корреляционного анализа, в основе которой лежит эргодическая гипотеза. [3]
Расчет случайных нагрузок от нерегулярных волн подразумевает определение их основных вероятностных характеристик-дисперсий ( стандартов), функций обеспеченности и спектральной плотности. [4]
Спектр равнодействующей нагрузки от нерегулярных волн на одиночную вертикальную опору при условии существенного преобладания инерционной составляющей нагрузки ( тС ( / стЙ17 5) может быть рассчитан как спектр чисто инерционной нагрузки на основе соотношений (2.85) - (2.86), если рассмотреть линейную систему волнение на поверхности - равнодействующая нагрузка на опору. [5]
При расчетах на воздействие нерегулярных волн массивы значений ординат волновых колебаний, статических и динамических реакций, вычисляемые с шагом At за весь интервал длительности счета, накапливаются и после окончания счета напряженно-деформированного состояния системы соответствующие массивы как случайные реализации с дискретными значениями ординат подвергаются статической и спектральной обработке по специально составленной подпрограмме. [6]
При изучении особенностей воздействия двухмерных нерегулярных волн на сквозные сооружения метод математического моделирования позволил численным путем впервые получить результаты, хорошо согласующиеся с данными экспериментальных исследований и основными положениями спектральной теории волн. [7]
При инженерных расчетах МНГС на воздействие нерегулярных волн возникает вопрос о влиянии вида спектра волн на количественные значения дисперсий характеристик волнового движения и их затухание с глубиной. [8]
При изучении движения пленки в условиях нерегулярных волн все измерения должны проводиться многократно, иначе измеренные значения могут иметь случайный характер. Таким образом, наиболее вероятные значения средней толщины пленки достаточно хорошо согласуются с теоретическими данными. [9]
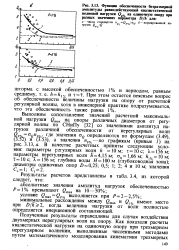 |
Функции обеспеченности безразмерной амплитуды равнодействующей квазистатической волновой нагрузки Q % на одиночную опору при разных значениях параметра D / h для. [10] |
Полученные результаты справедливы для случая воздействия двухмерных нерегулярных волн на опору. [11]
Поскольку опыт численного моделирования кинематических характеристик нерегулярных волн конечной высоты отсутствовал, то были вьшолнены расчеты реализаций волновых колебаний, скоростей и ускорений на разной глубине с использованием спектра Ю. М. Крылова [ см. формулу (2.106) ] при различных исходных данных ( табл. 2.9) и вычислены статистические и спектральные характеристики этих реализаций. [12]
В целом при инженерных расчетах нагрузок от нерегулярных волн на глубоководные сооружения сквозной конструкции вычисление стандартов скоростей и ускорений в разных уровнях по глубине может выполняться по обоим рассмотренным спектрам без больших погрешностей. [13]
Рассмотрим вероятностные характеристики квазистатических равнодействующих нагрузок от нерегулярных волн конечной высоты на одиночные ( 7VC 1) опоры различных диаметров. [14]
Лишь небольшое число работ посвящено изучению силового воздействия нерегулярных волн на отдельно стоящую цилиндрическую преграду ( С. [15]
Страницы: 1 2 3 4