Нерегулярная волна

Cтраница 2

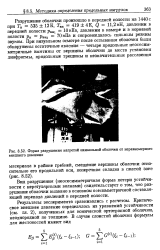Форма разрушения нагретой оживальной оболочки от неравномерного внешнего давления. [16]

Вид разрушения ( неосесимметричная форма потери устойчивости с нерегулярными волнами) свидетельствует о том, что разрушение оболочки вызвано в основном о се симметричной составляющей перепада давлений в передней полости. [17]

Результаты сравнительного расчета силовых нагрузок на основе линейной модели нерегулярных волн по (5.68), занижают расчетные величины Raaa примерно на 20 % по сравнению с (5.1), (5.11), (5.12) нелинейной моделью расчета регулярных волн. [18]

Вид спектра волновых колебаний безусловно влияет на характеристики воздействий нерегулярных волн на морские сооружения, но о степени этого влияния четких представлений пока нет. [19]

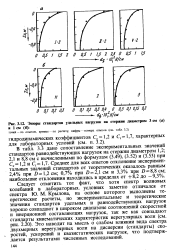Эпюры стандартов удельных нагрузок на стержни диаметром 3 см ( а и 1 см ( б. [20]

Это наводит на мысль о слабом влиянии вида спектра двухмерных нерегулярных волн на дисперсии ( стандарты) скоростей, ускорений и квазистатических нагрузок, что подтверждается результатами численных исследований. [21]

Анализ результатов всех описанных выше натурных и лабораторных исследований кинематики нерегулярных волн и их сопоставление с основными положениями спектральной теории волн ( двухмерных и трехмерных) позволяют выделить следующие, наиболее важные результаты. [22]

Рассмотрим теперь более подробно соответствие свойств и вероятностных характеристик реализаций нерегулярных волн, а также скоростей и ускорений частиц воды, полученных численным методом, основным положениям линейной спектральной теории, на которой этот метод базируется, а также имеющимся данным экспериментальных исследований. Для примера рассмотрим режим глубоководного волнения ( режим 7, спектр Ю.М.Крылова; Я100м; 4 15 м; т10с; Х156м), который будет использован в дальнейшем при численном исследовании динамики МНГС. [23]

До проведения широких численных исследований реакций сквозных конструкций при воздействии нерегулярных волн были выполнены методические численные исследования реакций одиночных ( JVC1) опор как с целью апробации метода математического моделирования, так и с целью выяснения ряда методических вопросов, таких, как влияние вида спектра волн на реакции конструкций, а также соответствие получаемых численным методом случайных реализаций реакций конструкций известным экспериментальным данным. [24]

Поскольку адалитическое решение для функции обеспеченности равнодействующий квазистатической нагрузки от двухмерных нерегулярных волн на одиночные опоры отсутствует из-за трудностей, связанных с необходимостью учета как нелинейности скоростной составляющей нагрузки, так и нелинейности ( конечной высоты) волн, то остановимся несколько подробнее на результатах экспериментальных и численных исследований этой функции. [25]

В отличие от неоднозначности видимых амплитуд реализаций давлений и скоростей частиц нерегулярных волн, амплитуды спектральных составляющих давлений и скоростей на разной глубине в области частот максимума спектра хорошо подчиняются законам классической гидродинамики как для натурных трехмерных волн [10, 20,66], так и для двухмерных волн в лаборатории ( см. рис. 2.19), подтверждая достоверность гипотезы суммирования элементарных волн. [26]

Прежде всего, как натурные, так и лабораторные исследования нагрузок от нерегулярных волн показали, что между абсолютными значениями величин нагрузок и параметрами видимых волн нет однозначной зависимости [10, 41, 51], причем при фиксированной высоте волны значения нагрузок по измерениям в натуре могут отличаться до десяти раз; разброс экспериментальных данных в натурных условиях при трехмерном волнении больше, чем при двухмерном волнении в лаборатории. [27]

Таким образом, возможность объективного применения тех или иных аналитических спектров для расчетов кинематики нерегулярных волн может быть установлена только в результате сопоставления теоретических решений с результатами экспериментальных исследований. [28]

Основы подобного метода динамического расчета глубоководной морской стационарной платформы ( МСП) на воздействие двухмерных нерегулярных волн изложены в работе А. Дэлея и др. ( 1977), в которой для упрощения вычисления нагрузок от волн решетчатая конструкция опорной части МСП заменяется эквивалентными по волновой нагрузке экранами, сосредоточенными на одной вертикальной оси, что не позволяет корректно учесть влияние пространственной протяженности сооружения на его динамические реакции. [29]

В работе [26] впервые была экспериментально доказана зависимость функций обеспеченности динамических реакций податливых сквозных сооружений при воздействии нерегулярных волн от параметра T / i, чем они существенно отличаются от функций обеспеченности квазистатических нагрузок от волн. [30]

Страницы: 1 2 3 4