Нерегулярная волна

Cтраница 3

Так как в настоящее время отсутствуют строгие аналитические методы расчета, функций обеспеченности даже случайных квазистатических равнодействующих нагрузок от нерегулярных волн конечной высоты на отдельно стоящие жесткие опоры ( см. разд. [31]

Обоснования рекомендаций по выбору расчетной высоты регулярных волн, эквивалентных по глубине вызванного ими местного размыва защитной наброски воздействию последовательности нерегулярных волн с известными средними характеристиками, в настоящее время отсутствуют и требуют проведения специальных исследований. [32]

Завышение значений стандартов нагрузки JQC; для опор малых диаметров, когда преобладает скоростная составляющая нагрузки, объясняется учетом конечной высоты нерегулярных волн в методе математического моделирования. Для диаметров Dl0-2 0м ( D / h 0 24 - 0 48), характерных для опорных стоек реально проектируемых и строящихся МСП, расхождение составляет в среднем 5 %, что приемлемо для инженерных приложений. [33]

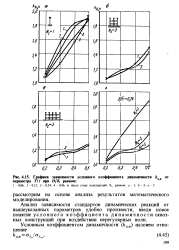Графики зависимости условного коэффициента динамичности Агд н от параметра 77 т при D / h, равном. [34]

Анализ зависимости стандартов динамических реакций от вышеуказанных параметров удобно произвести, введя новое понятие условного коэффициента динамичности сквозных конструкций при воздействии нерегулярных волн. [35]

На рис. 64 показаны напряжения, возникающие в трубопроводах с сечениями 1020X20, 800X18 и 325X14 мм при воздействии на ТС нерегулярных волн различной интенсивности. Расчеты проведены для условий, указанных в ранее приведенных примерах. [36]

К сожалению, в настоящее время отсутствуют аналитические решения, позволяющие вычислить функции распределения ( обеспеченности) ординатных и амплитудных значений равнодействующей нагрузки от нерегулярных волн на жесткую вертикальную опору. В рамках линейной спектральной теории решение такой задачи невозможно. Поэтому информация о функции обеспеченности равнодействующей нагрузки на опору может быть получена либо экспериментальными, либо численными методами, как будет показано далее. [37]

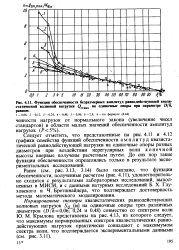Функция обеспеченности безразмерных амплитуд равнодействующей квази статической волновой нагрузки Qama на одиночные опоры при параметре Djh, равном. [38]

Следует отметить, что представленные на рис. 4.11 и 4.12 графики семейства функций обеспеченности амплитуд квазистатической равнодействующей нагрузки на одиночные опоры разных диаметров при воздействии нерегулярных волн конечной высоты впервые получены расчетным путем. [39]

Как видно из рис. 5.22, кривые изгибающих моментов ( б) и ( г) представляют собой сумму двух видов колебаний: вынужденных колебаний с периодами нерегулярных волн и резонансных колебаний импульсного характера с периодом т 1 6 с. Отделим эти колебания друг от друга. [40]

В сводных табл. 4.5 и 4.6 приведены значения стандартов квазистатических равнодействующих нагрузок, а также статических и динамических перемещений верха одно - и многостоечных конструкций при воздействии нерегулярных волн. [41]

Поскольку, согласно формулам (5.13) и (5.14), равнодействующая волновая нагрузка и опрокидывающий момент на цилиндр линейно зависят от амплитуды ( Н / 2) гармонических волн, то решение для нерегулярных волн может быть получено линейной суперпозицией соответствующих гармонических составляющих. [42]

Для статических реакций отдельной опоры в случае резкого преобладания скоростной составляющей нагрузки ( рис. 4.9) характерна существенная асимметрия между гребнями и впадинами - гребни выше и уже впадин, что объясняется учетом конечной высоты нерегулярных волн. При резком преобладании инерционной составляющей нагрузки асимметрия гребней и впадин статических реакций невелика, что также подтверждается данными опытов. [43]

Q ( t) и M ( t) линейно зависят от амплитуд гармонических волн, а распределение ординат волновых колебаний при нерегулярном волнении подчиняется нормальному закону, то и случайные функции равнодействующей нагрузки и опрокидывающего момента от воздействия нерегулярных волн на цилиндр большого диаметра будут также подчиняться нормальному закону распределения. [44]

Последний спектр принят к рассмотрению, так как он описывает полностью развитое волнение и широко используется за рубежом в инженерных приложениях, а его недостаток, заключающийся в невозможности строгого аналитического определения дисперсии ускорений частиц, может быть преодолен при использовании численного метода расчета кинематических характеристик нерегулярных волн, разработанного автором. [45]

Страницы: 1 2 3 4