Плазменная волна
Cтраница 1
Медленная плазменная волна усиливается релятивистским пучком, и далее трансформируется в ТЕМ-моду выходного металлического коаксиального волновода и излучается выходным коаксиальным рупором 5 большого сечения. [1]
Длина плазменной волны обычно имеет порядок нескольких периодов элементарной ячейки, а угол рассеяния падающего электрона очень мал в сравнении с углами брэгговских отражений. [2]
Период плазменной волны, которая рассеивается на электронном пучке, определяется дисперсионными свойствами плазмы. Параметром, определяющим эффективность преобразования кинетической энергии пучка в энергию коротковолнового электромагнитного излучения является величина ае; еЕ / ( mew), где Е и uj - напряженность и частота электрического поля электромагнитной волны накачки. [3]
Раскачка плазменных волн при подобного рода не-устойчивостях приводит к тому, что энергия возбуждающих частиц быстро уходит к плазменным волнам. Это вызывает также быстрое выравнивание всякого рода инверсностей в заселенности уровней ( сглаживание горба пучка, заполнение конуса высыпания) до тех пор, пока причина, возбуждающая неустойчивость, не исчезнет. [4]
Если длина плазменной волны сравнима с дебаевским радиусом ( k - l / de), то она столь быстро затухает, что, по существу, нельзя вообще говорить о ее существовании. Однако, если k ildef затухание продольных плазмонов экспоненциально мало. [5]
Представим себе плазменную волну и заряд, движущийся со скоростью, несколько меньшей фазовой скорости волны и направленной вдоль ее волнового вектора. Тогда он будет довольно долго находиться вблизи, например, максимума амплитуды волны. [6]
Наряду с плазменными волнами, связанными с колебаниями электронов, в плазме могут распространяться также и волны, в которых испытывают существенные колебания как электронная, так и ионная плотности. [7]
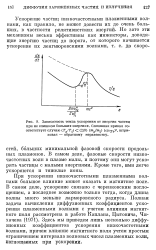 |
Зависимость темпа ускорения от энергии частиц при не слишком больших энергиях. Сплошная кривая соответствует случаю ( Tg / TjX ( 2 / 9 ( т & 1т ( с / иГе 2, штриховая - обратному неравенству. [8] |
Ускорение частиц низкочастотными плазменными волнами, как правило, не может довести их до очень больших, в частности релятивистских энергий. [9]
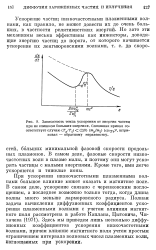 |
Зависимость темпа ускорения от энергии частиц при не слишком больших энергиях. Сплошная кривая соответствует случаю ( Tg / TjX ( 2 / 9 ( т & 1т ( с / иГе 2, штриховая - обратному неравенству. [10] |
При ускорении низкочастотными плазменными волнами большое влияние может оказать и магнитное поле. В самом деле, ускорение связано с черепковским поглощением, а последнее возможно только тогда, когда длина волны много меньше ларморовского радиуса. [11]
Вывод о затухании плазменных волн получен из обратимого по времени кинетического уравнения Власова. Это затухание не сопровождается ростом энтропии, представляя собой термодинамически обратимый процесс. Оно может быть установлено непосредственно из уравнений механики. [12]
Рассмотрим поэтому рассеяние плазменных волн на шубе тепловых ионов более подробно. Пусть частота и волновой вектор падающей волны равны со и А /, а рассеянной волны - со и / с. Так как рассеянная волна может отличаться от падающей волны и по типу, то дисперсионные соотношения со ( А /) и со ( fc) тоже различны. [13]
Только после изотропизации плазменных волн начинается перекачка энергии вдоль спектра от больших волновых чисел к малым. При этом происходит и перераспределение направлений волновых векторов; но для изотропной турбулентности такое перераспределение значения не имеет. [14]
Поскольку фазовая скорость плазменных волн часто много меньше скорости света, относительное изменение разности волновых векторов электромагнитных волн заметно ( в c / Vp раз) больше изменения их частот. Поэтому волновые векторы преимущественно поворачиваются, мало изменяя свою величину. Иными словами, высокочастотные электромагнитные волны в турбулентной плазме испытывают специфическое рассеяние по направлениям распространения и относительно небольшое изменение частоты. [15]
Страницы: 1 2 3 4