Плазменная волна

Cтраница 2

Если плотность энергии плазменных волн велика, то возможно, что последний член (4.27) также окажется существенным и будет превышать члены с затуханием. [16]

Новым результатом является затухание плазменных волн. На первый взгляд этот результат представляется парадоксальным. Выше мы видели, что диссипативные процессы были связаны с молекулярными столкновениями и возникающим при этом обменом импульсом. Найденное выше затухание плазменных волн ( так называемое затухание Ландау) имеет другую природу. [17]

Физической причиной возникновения затухания плазменных волн является обратный эффект Черепкова. [18]

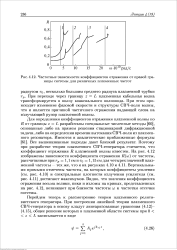Частотные зависимости коэффициентов отражения от правой границы системы для различных плазменных частот. [19]

Для определения коэффициентов отражения плазменной волны по R от границы z L разработаны специальные численные методы [60], основанные либо на прямом решении стационарной дифракционной задачи, либо на определении времени вытекания СВЧ-поля из плазменного резонатора. [20]

Частица ускоряется в нем плазменной волной, возбуждаемой с помощью двух коллинеарных лазерных пучков в неоднородной плазме. В случае, когда излучение одного из лазерных пучков является широкополосным, возбуждаемое в плазме электростатическое поле Е ( х, t) также будет иметь большую спектральную ширину. [21]

Близость структуры поля этой части плазменной волны к структуре ТЕМ-волны коаксиального излучающего устройства, большая фазовая скорость, близкая к скорости света, обеспечивают высокую эффективность вывода энергии плазменной волны в коаксиальное излучающее устройство. Применение коаксиального выходного волновода обеспечивает возможность эффективного вывода илучения в широкой полосе частот. [22]

Очевидно, что мощность излучения плазменных волн определяется интегрированием вероятности распада электромагнитных волн по всему их спектру от сотш до самых больших частот. [23]

В силу условия kae декремент затухания плазменных волн действительно оказывается экспоненциально малым. Он возрастает с уменьшением длины волны и при kae - 1 ( когда формула ( 32 7) уже неприменима) становится того же порядка величины, что и частота, так что понятие о распространяющихся плазменных волнах теряет смысл. [24]

Задача 3.3. Получить дисперсионное соотношение для плазменных волн, которые отвечают движению электронной компоненты в плазме. [25]

Задача 3.38. Получить дисперсионное соотношение для плазменных волн в случае, когда плотность энергии, заключенной в плазменных колебаниях плазмы, заметна. Считать, что напряженность электрического поля, обусловленного плазменными колебаниями, мало изменяется на расстояниях порядка длины волны колебаний. [26]

Комптоновское рассеяние возможно для всех видов плазменных волн, а то обстоятельство, что в этом случае происходит заметное изменение частоты, означает, что здесь легко выполняются условия трансформации одного вида плазменных волн в другие. Например, ионнозвуко-вые волны при рассеянии па релятивистских электронах могут превращаться в ленгмюровские, а также непосредственно в электромагнитные волны, или наоборот. [27]

Ионпозвуковая турбулентность возбуждается и другими видами плазменных волн. [28]

Подобным образом могут возбуждаться и другие моды плазменных волн, но для них величина Q очень мала. Например, для ионнозвуковых волн QB х ( melm Q1, для вистлеров Qw ( cope / co e) 4 Ql Величину (4.57) следует подставить во все формулы теории турбулентности продольных плазмонов для того, чтобы получить свойства этой турбулентности в том случае, когда она возбуждается изотропным высокочастотным излучением. Такой процесс действительно существует и мы его рассмотрим в следующем параграфе. Однако он весьма медленный в сравнении со многими другими нелинейными процессами, возникающими из-за возбуждения плазменных колебаний. [29]

Важным является вопрос и о способе возбуждения интенсивной плазменной волны, которая может играть роль ондулятора. [30]

Страницы: 1 2 3 4