Одиночная волна

Cтраница 1

Одиночная волна § 252 сюда включается как частный случай. [1]

Одиночную волну Русселя можно рассматривать как предельную форму колебательной полны Стокса установившегося вида, причем, так как длина волны должна быть большой сравнительно с глубиной канала, далеко лежащие друг от друга возвышения практически будут независимы друг от друга. Примененные Стоксом приближенные методы оказываются, однако, непригодными, если длина волны намного превосходит глубину, поэтому дальнейшие исследования об одиночных полнах установившегося вида развивались в другом направлении. [2]

Распространение одиночных волн изучено лучше всего. [3]

Движение в крайних частях одиночной волны может быть представлено одной очень простой формулой. [4]

Описанный процесс представляет распространение одиночной волны отклонения; после прохождения такой волны точки струны возвращаются в свое исходное положение на оси абсцисс. [5]

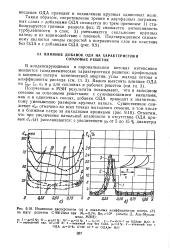Изменение дисперсности ( а и локальных коэффициентов потерь ( б по шагу решетки С-9012 Авл при M. i 0 74. Rei. 106 ( опыты Д. Аль-Мухам. [6]

ОДА приводит к подавлению крупных одиночных волн. Таким образом, сопротивление трения в двухфазных пограничных слоях с добавками ОДА снижается по трем причинам: 1) стабилизируется граница раздела фаз; 2) снижается интенсивность турбулентности в слое; 3) уменьшается скольжение крупных капель и их взаимодействие с пленкой. [7]

Плотность энергии в каждой одиночной волне бесконечно мала и одинакова для всех волн. [8]

Показано, что нагрузка от одиночной волны на 35 % больше, чем от линейных волн. Метод требует применения самых мощных современных ЭВМ с большим быстродействием. [9]

В настоящее время под солитоном понимается одиночная волна, имеющая вид импульса, которая распространяется в нелинейной среде с дисперсией. Солитоны обладают странными свойствами, которые делают их похожими в некотором отношении на частицы. [10]

Это допущение можно считать оправданным в случае одиночной волны или серии волн, у которых расстояние между соседними гребнями достаточно велико. [11]

Физически установившиеся волны представляют собой бесконечные суммы прямых и обратных одиночных волн, отраженных от обоих концов линии. [12]

Приближенная теория замеченного при наблюдениях и экспериментах явления одиночной волны была дана Буссинеском и Рэйли, и, например, формула, даваемая этой теорией для скорости волны, совпала с эмпирической. Точное решение задачи было дано в 40 - х годах XX в. [13]

Очевидно что для таких сред невозможно устойчивое распространение одиночных волн, поскольку стационарное однородное состояние неустойчиво - по отношению к сколь угодно слабым возмущениям. [14]

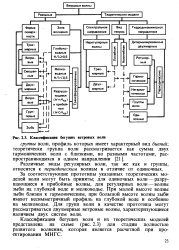Классификация бегущих ветровых воли. [15]

Страницы: 1 2 3 4