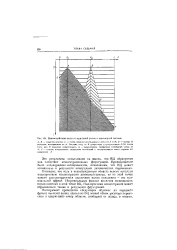
Одиночная волна

Cтраница 2

За соответствующие прототипы указанных теоретических моделей волн могут быть приняты; для одиночных волн - разрушающиеся и прибойные волны, для регулярных волн-волны зыби на глубокой воде и мелководье. При малой высоте волны зыби близки к гармоническим, при большой высоте волны зыби имеют несимметричный профиль на глубокой воде и особенно на мелководье. Для групп волн в качестве прототипа могут рассматриваться двухмерные ветровые волны, характеризующиеся наличием двух систем волн. [16]

Для рассматриваемой задачи существует предельный случай, когда периодическое решение вырождается в одиночную волну. Эта неоднородность и может быть интерпретирована как макрокластер на поверхности катализатора, например пятно СО на 02 либо, наоборот, пятно 02 на СО. [17]

При разрушении плотин или любых перегородок, поддерживающих высокий уровень воды, появляется одиночная волна ( волна Скотт - Русселя), профиль которой целиком располагается над поверхностью. При достаточной глубине эта волна перемещается, устойчиво сохраняя свою форму и неся большой запас энергии. При разрушении большой плотины одиночная волна может принести много бедствий на больших расстояниях вниз по течению. [18]

Асимметричная рябь возникает в приурезовой полосе мелководья благодаря действию деформированной после забурунивания или одиночной волны. [19]

Как отмечалось в этих работах, существует критическое значение кривизны Кнр изогнутого фронта одиночной волны возбуждения. Если кривизна фронта К превышает величину кр, устойчивое распространение волны невозможно. В работе [84] предложена приближенная процедура расчета медленно вращающихся спиральных волн, основывающаяся на требовании, чтобы на границе ядра кривизна фронта была равна критической. [20]

Образование стоячих волн при колебаниях веревки, закрепленной на одном конце. [21]

Если мы сделаем рукой резкое движение вверх и вниз, то по веревке побежит одиночная волна, которая отразится от закрепленного конца и побежит обратно, достигнет руки отразится от нее и опять побежит к стене. Если подбрасывать веревку периодически, то получаются два ряда волн, налагающихся друг на друга: волны, идущие к стене, и отраженные волны, идущие от стены. Наложение этих волн приводит к сложной и изменяющейся форме колебаний веревки, но при некоторых значениях периода подбрасываний мы получим так называемые стоячие волны. Мы увидим, что отдельные участки веревки находятся в покое, другие же испытывают максимальное смещение вверх и вниз относительно ее натянутого положения. Те точки веревки, которые не совершают колебаний, называются узлами, а те точки, в которых амплитуда смещений максимальна, - пучностями колебаний. [22]

Для средних глубин производится интерполяция с учетом теорий Стокса и Митчелла и усовершенствованной теории одиночной волны. При интерполировании за основу берется теория Стокса, а в уравнения, характеризующие профиль волны, вводятся дополнительные члены более высокого порядка. [23]

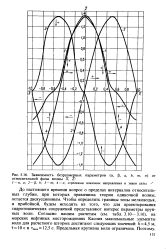Зависимость безразмерных параметров ( а. [24]

До настоящего времени вопрос о пределах интервалов относительных глубин, при которых применима теория одиночной волны, остается дискуссионным. Чтобы определить границы зоны мелководья, и прибойной, будем исходить из того, что для проектирования гидротехнических сооружений представляют интерес параметры крупных волн. Согласно нашим расчетам ( см. табл. 3.10 - 3.16), на морских нефтяных месторождениях Каспия максимальные элементы волн для расчетного шторма достигают следующих значений: Л 4 5 м, т 10 с и ттах 12 5 с. Предельная крутизна волн ограничена. [25]

Взаимодействие волн от водителей ритма в одномерной системе А. В - водители ритма. С - точка первого Столкновения волн от А В. D - захват В волнами, исходящими из А. Система вол it от В существует в треугольнике DEH после того, как В перестал существовать. С - исчезновение синфазных колебаний слева от A. F - полное исчезновение синфазных колебания и синхронизация всего отрезка OL водителем А. [26]

Очевидно, что если в невозбуждепную область внести локально надпороговую концентрацию автокатализатора, то из этой точки начнет распространяться одиночная волна окисления - это тривиальный эффект. Нетривиальным фактом является возможность возникновения в этой точке ВЦ. Надпороговая концентрация может образоваться также в результате флуктуации. [27]

Описанная выше постановка задачи была, в частности, использована Leibovich, Kribus [1990] при поиске решений (4.72) в виде нелинейных стоячих периодических и одиночных волн. [28]

Эпюры линейной нагрузки от волн при Л13 5 м ( Я110 м, диаметр 530, 920 мм, рассчитанные соответственно по СНиП - 82 и обобщенному методу. [29]

Для получения равнодействующей волновой нагрузки на сваю и стержень требуется подставить ( выражения - значения) скоростей и ускорений из теории одиночных волн и теории волн Стокса второго порядка приближения в формулы (1.1) и (1.2) и проинтегрировать по всей длине, что сопряжено с большими трудностями, так как имеются частные решения. [30]

Страницы: 1 2 3 4