Синусоидальные волны

Cтраница 2

Простейшим примером периодических звуковых волн являются синусоидальные волны. В акустике такие звуки называются простыми или чистыми тонами. Однако упругие волны, возбуждаемые реальными источниками звука, представляют собой совокупность синусоидальных волн с различными частотами и амплитудами. [16]

Зависимость кинетического фактора от величины волнового вектора для макроскопически изотропной системы. [17]

Фурье) частных решений, описывающих синусоидальные волны. [18]

Вещественная часть этих приближенных решений - бегущие синусоидальные волны, если, т вещественны. [19]

Простейшим примером периодических звуковых волн могут служить синусоидальные волны. В акустике такие звуки называются простыми, или чистыми, тонами. Однако упругие волны, возбуждаемые реальными источниками звука, представляют собой совокупность синусоидальных волн с различными частотами и амплитудами. [20]

Профили возбужденных волн. [21]

Максимально возможной частоте в этом диапазоне отвечают синусоидальные волны. По мере уменьшения частоты форма волн изменяется, как это показано схематически на рис. 4.5, а-в. Интересно, что в целом возбужденные и естественные двумерные волны практически тождественны. [22]

Осциллограмма пульсаций скорости случайных ( естественных возмущений в ламинарном пограничном слое на плоской пластинке, обтекаемой воздухом в продольном направлении.| Снимки пограничного слоя на вертикальной пластинке при свободном конвективном течении. [23]

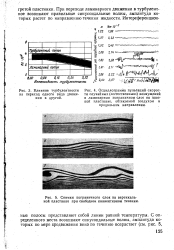
При переходе ламинарного движения в турбулентное возникают правильные синусоидальные волны, амплитуда которых растет по направлению течения жидкости. [24]

Уравнения ( 40) и ( 42) определяют синусоидальные волны, которые в любой момент времени описывают возмущение всей ( неограниченной) среды. [25]

Как было показано раньше, две бегущие в противоположном направлении синусоидальные волны с одинаковой частотой и амплитудой образуют стоячую волну. При отражении синусоидальной волны, бегущей по трубе, от закрытого ( или открытого) конца всегда в трубе образуется стоячая волна, если при отражении не происходит потерь энергии. Таким образом, в за - t - 0 крытой с обоих концов трубе или на струне с закрепленными концами возможны гармонические колебания в виде стоячих волн, при которых у закрытого конца трубы имеется узел волны смещения; то же наблюдается и у закрепленных концов струны. [26]

Частным случаем таких плоских волн могут являться часто используемые на практике чисто синусоидальные волны, при которых напряженности Е и Н в каждой точке пространства могут совершать только чисто гармонические колебания. [27]

Для исследования электродной кинетики предлагались методы, ис-пользующие как квадратные [557 - 559], так и синусоидальные волны [530]; выведены уравнения для малых отклонений от равновесия при нулевой составляющей постоянного тока. Стационарное циклическое состояние практически устанавливается за 100 периодов. [28]

Для экспериментального исследования капиллярных волн обычно используют колеблющуюся полоску, генерирующую, по существу, синусоидальные волны. [29]

В этом случае сигнал перемещается в среде, не изменяя своей формы, так как все синусоидальные волны, образующие эту группу, имеют одинаковые фазовые скорости, равные скорости сигнала. [30]

Страницы: 1 2 3 4