Синусоидальные волны
Cтраница 3
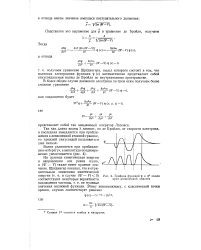 |
Графики функций oj и з2 около края дозволенной области. [31] |
Шредингера, смысл которого состоит в том, что волновая электронная функция т з ( х) математически представляет собой синусоидальные волны де Бройля во внутриатомном пространстве. [32]
На начальном участке, поверхность пленки гладкая, затем по периметру трубы появляются отдельные возмущения, из которых далее по течению формируются синусоидальные волны постоянной длины и с прямым фронтом. С увеличением числа Рейнольдса пленки характер поверхности изменяется, волны двигаются с различной скоростью, имеют различные высоту и направление фронта. В дальнейшем появляются капиллярные волны и, наконец, отдельные кольцевые волны большой высоты. С изменением структуры волн меняются и закономерности массо - и теплопе-реноса в пленке и силы трения на границе раздела фаз. [33]
В идеальном случае линии без потерь ( г 0, g 0) при режимах с нулевой средней мощностью ( холостой ход, короткое замыкание, чисто реактивная нагрузка) распределения мгновенных значений напряжения и тока представляют собой стоячие синусоидальные волны, сдвинутые между собой по длине линии на четверть длины волны, а по фазе на четверть периода. [34]
Исходя из изложенного, на основании ( 8 - 9), ( 8 - 10) и ( 8 - 13), на рис. 8 - 7 изображены огибающие амплитуд бегущих полей краевого эффекта. Затухающие синусоидальные волны бегущих полей краевого эффекта расположены между этими огибающими. [35]
В приведенном выше выражении от времени зависит только первый член. Две синусоидальные волны когерентны, если их частоты одинаковы ( о) 1 ( о2), и некогерентны, если их частоты различны. [36]
В приведенном выше выражении от времени зависит только первый член. Две синусоидальные волны когерентны, если их частоты одинаковы ( о1со2), и некогерентны, если их частоты различны. [37]
Поэтому две синусоидальные волны когерентны, если их частоты одинаковы, и некогерентны, если их частоты различны. [38]
Сделанное в конце § 13.5 замечание не исключает возможности распространения с постоянной скоростью волн специального вида. Особую роль для теории играют синусоидальные волны / sin k ( x - ct) X const. [39]
Любое неравномерное движение электрических зарядов вызывает электромагнитное излучение. Если электрические заряды совершают гармонические колебания, то излучаются синусоидальные волны. За каждый период колебаний излучается отдельная электромагнитная волна. На рис. 22.2 показана моментальная фотография электромагнитной волны, распространяющейся вдоль оси ОХ. Векторы Е и Н взаимно перпендикулярны и расположены в плоскостях, перпендикулярных направлению распространения волны так, что кратчайший поворот от Е к Н происходит по правилу правого винта. [40]
Неравенство (26.22) 3 является следствием отражений от краев Y О, L и наложения волн. Решение (26.12) выражается суммой решений (26.11), которые представляют собой две синусоидальные волны. Первая из них движется в направлении, ортогональном к плоскости - а Х Y const, а вторая - в направлении, ортогональном к плоскости - аХ - ( 3Y const. [41]
Авторы [6] высказали гипотезу, что если fy0 5, то синусоидальные волны, вырастающие на поверхности раздела фаз, касаются верхней стенки трубы раньше, чем провал между волнами достигает дна трубы. Из этого предположения следует, что для / 1г0 5, переход от расслоенного течения к перемежающемуся более вероятен, чем к кольцевому. [43]
Тот же эффект можно наблюдать и на осциллографе, который просто показывает сумму токов двух генераторов. Если частота пульсаций сравнительно мала, то мы просто видим, как на экране перед нами проходят синусоидальные волны, амплитуда которых пульсирует, но если сделать пульсации более быстрыми, то мы увидим нечто похожее на то, что показано на фиг. По мере увеличения разницы между частотами вершины сближаются все больше и больше. Если амплитуды не равны друг другу, если мы один сигнал сделаем слабее другого, то образуется волна, амплитуда которой, как это и ожидается, никогда не становится равной нулю. [44]
Хотя гармонические колебания часто встречаются, однако большинство периодических явлений ( ср. V, § 4, п 3) носит более сложный характер, представляя собой наложение ( суперпозицию) синусоидальных колебаний. Синусоидальные волны этой функции налагаются тогда геометрически одна на другую или, как говорят, суперпонируются. При таком наложении мы будем предполагать, что частоты ( а стало быть, и периоды) налагаемых колебаний все различны, потому что суперпозицию двух гармонических колебаний одной и той же круговой частоты о мы уже изучили в п 1-она дает опять-таки гармоническое колебание, но с измененной амплитудой и начальной фазой. [45]
Страницы: 1 2 3 4