Простые волны
Cтраница 2
В отличие от случая малых возмущений, рассмотренного в § 26, где все простые волны имели одну и ту же по величине скорость распространения, равную скорости звука в невозмущенном газе, в разбираемом сейчас случае простых волн, несущих конечные по интенсивности возмущения, скорости распространения по отношению к газу, равные по абсолютной величине местной скорости звука, не одинаковы для различных волн данного семейства. [16]
В отличие от случая малых возмущений, рассмотренного в § 22, где все простые волны имели одну и ту же по величине скорость распространения, равную скорости звука в невозмущенном газе, в разбираемом сейчас случае простых волн, несущих конечные по интенсивности возмущения, скорости распространения по отношению к газу, равные по абсолютной величине местной скорости звука, не одинаковы для различных волн данного семейства. [17]
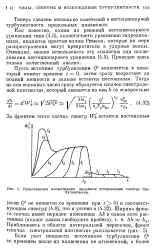 |
Качественная иллюстрация динамики установления спектра турбулентности. [18] |
Как известно, одним из решений нестационарного уравнения типа (4.5), аналогичного уравнению гидродинамики, являются простые волны Римана, которые по мере распространения могут превратиться в ударные волны. [19]
Для частного вида движений, обладающих свойством dy / dt сду / дх, с const ( простые волны), уравнение ( 15) переходит в изученное в § 1 гл. [20]
Поэтому рассматриваемый класс течений играет в теории стационарного плоского ( сверхзвукового) движения такую же роль, какую играют простые волны в теории нестационарного одномерного движения. Ввиду этой аналогии эти течения тоже называют простыми волнами. В частности, волну разрежения, соответствующую случаю f2 - 0, называют центрированной простой волной. [21]
Поэтому рассматриваемый класс течений играет в теории стационарного плоского ( сверхзвукового) движения такую же роль, какую играют простые волны в теории нестационарного одномерного движения. Ввиду этой аналогии эти течения тоже называют простыми волнами. В частности, волну разрежения, соответствующую случаю / 2 0, называют центрированной простой волной. [22]
Поэтому рассматриваемый класс течений играет в теории стационарного плоского ( сверхзвукового) движения такую же роль, какую играют простые волны в теории нестационарного одномерного движения. Ввиду этой аналогии эти течения тоже называют простыми волнами. В частности, волну разрежения, соответствующую случаю f2 s 0, называют центрированной простой волной. [23]
Поэтому рассматриваемый класс течений играет в теории стационарного плоского ( сверхзвукового) движения такую же роль, какую играют простые волны в теории нестационарного одномерного движения. Ввиду этой аналогии эти течения тоже называют простыми волнами. В частности, волну разрежения, соответствующую случаю f2 0, называют центрированной простой волной. [24]
Целесообразность разложения сложной волны на сумму именно монохроматических составляющих обусловлена не только тем, что монохроматические волны - это наиболее простые волны и их свойства хорошо известны. [25]
Rem pFL / vm оо) исследованы звуковые волны, слабые разрывы ( см., например, В. Н. Жигулев, 1959), простые волны ( см. А - И. [26]
Если вообразить ударный фронт разрежения, или переход из состояния 1 в состояние 0, то для него все рассуждение станет обратным: он будет испускать вперед себя звуковые волны и размоется в пространстве, теряя свойства разрыва, а звуковые, или простые волны, бегущие сзади, не догонят и, следовательно, не усилят его. [27]
Простыми волнами называют важный тип решения основных уравнений. Простые волны могут быть введены различными, но в основном эквивалентными путями. Каждая линия w отображается согласно определению на одну точку s, 0 плоскости напряжений. [28]
Для изотропного материала одна из этих волн является волной с круговой поляризацией, а две другие - плоскополяризованными. Плоскополяризованные простые волны, представленные уравнениями (3.57) и (3.58), автор не будет рассматривать детально. Фор-ма этих волн будет рассмотрена для амплитуд, которые являются малыми, но не инфинитезимальными. [29]
Учитывая неравенства (13.30), приходим к выводу, что неравенство (13.41) не выполняется в данном случае, поскольку Р, v и с - положительные величины. Таким образом, простые волны ежа-тия неустойчивы. [30]
Страницы: 1 2 3 4