Плоские волны

Cтраница 1

Плоские волны возбуждаются колеблющейся пластиной, если ее поперечные размеры значительно превосходят длину волны. Волновые поверхности плоской волны имеют вид параллельных плоскостей. [1]

Плоские волны с данным k2 различного направления статистически равновероятны. [2]

Плоские волны нормируем на объем V и наложим на них условия периодичности. Благодаря тому, что электронные состояния с энергией, меньшей энергии Ферми, заняты, суммирование в ( 64 2) соответственно ограничено снизу. Разумеется, такое ограничение суммирования снизу не является строго последовательной операцией. В действительности нужно рассматривать многоэлектронную задачу. Купер сводит эту проблему к задаче двух взаимодействующих электронов на фоне заполненной ферми-сферы. [3]

Плоские волны в безграничном однородном газе соответствуют, по существу, рассмотренному выше случаю, если считать А постоянной, а х выбрать в направлении, перпендикулярном волновому фронту. [4]

Плоские волны в природе невозможны, хотя бы по причине их безграничной протяженности в поперечном сечении. Но плоские волны можно осуществить с определенной, как угодно далеко идущей степенью приближения при помощи того же приема, который мы раньше применяли для изотропных сред. Выбрав t достаточно большим, мы можем на волновой поверхности выделить участок произвольной величины, размеры которого малы сравнительно с расстоянием его от О и который может считаться плоским. Тогда вся волновая поверхность окажется составленной из таких плоских участков, для каждого из которых справедливы законы распространения плоских волн. [5]

Плоские волны распространяются в однородном немагнитном анизотропном диэлектрике. [6]

Плоские волны возникают, например, в закрытом поршнем цилиндре с газом, когда поршень совершает колебания. [7]

Плоские волны представляют собой простейший случай волнообразного процесса. [8]

Плоские волны являются частным случаем волн. Вообще говоря, характер волн более сложен. Например, волны, распространяющиеся от брошенного в воду камня, имеют вид расходящихся кругов. Для наглядности описания волн пользуются понятием волновых поверхностей. Волновой поверхностью называется совокупность ( геометрическое место) точек, колеблющихся в одинаковой фазе. Каждому значению фазы отвечает своя волновая поверхность. Волновые поверхности могут иметь любую форму. В простейших случаях они имеют вид плоскости или сферы. Соответственно волна в этих - случаях называется плоской или сферической. В плоской волне волновые поверхности представляют собой систему параллельных друг другу плоскостей, в сферической волне - систему концентрических сфер. [9]

Система координат для анализа плоской волны. [10]

Плоские волны, у которых плоскости равных амплитуд не параллельны плоскостям равных фаз, называются неоднородными плоскими волнами. [11]

Плоские волны обладают, как видим, весьма простыми свойствами. Возникает идея представить волну в волноводе как результат наложения ( суперпозиции) плоских волн. [12]

Плоские волны на межфазной поверхности, причем их векторная амплитуда совпадает по направлению с основным конвективным потоком. [13]

Плоские волны не являются единственным решением этих волновых уравнений. Другим решением являются так называемые гауссовы пучки, которые мы рассмотрим в гл. [14]

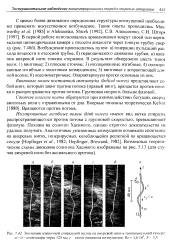Эволюция одиночной спиральной полны па вихревой нити в тангенциальной каморе. а - д - стоп-кадры чере-з 125 мс. е схема движения возмущения. Re - 1 6 - 10, S - 3 5. [15]

Страницы: 1 2 3 4