Симметричный волчок

Cтраница 3

Поскольку у симметричного волчка имеются два типа вращения, приходится ввести два вращательных квантовых числа / и К. Оба они могут принимать любое целочисленное значение; важно только, чтобы К не превышало J. Квантовое число / ( соответствует вращению вокруг единственной оси a, a / - вращению молекулы относительно осей бис. Вращение молекулы типа симметричного волчка относительно единственной оси не приводит к изменению диполь-ного момента относительно направления падающего излучения, Р и с. [31]

Молекулы типа симметричного волчка могут совершать низкочастотные крутильные колебания. Возможно ограниченное внутреннее вращение одной группы атомов относительно другой. Поскольку в таких молекулах внутреннее вращение не изменяет дипольного момента, его нельзя обнаружить непосредственно по спектру поглощения. Однако вследствие изменения во взаимодействии симметричных групп, например в CH3SiH3 или CH3CF3, при отклонении атомов от положений равновесия может возникать влияние крутильных колебаний на момент инерции относительно одной из осей. [32]

Рассмотрим случай симметричного волчка. [33]

В случае симметричного волчка вектор Р уже не обязан быть перпендикулярным оси волчка, даже если момент количества движения электронов равен нулю; в общем случае вектор Р имеет постоянную составляющую Рг в направлении оси волчка. Эта диаграмма в существенных чертах та же, что и в случае двухатомной молекулы, в которой учитывается вращение электронов вокруг оси молекулы. [34]

Рассмотрим поведение симметричного волчка с одной неподвижной точкой, находящегося в однородном поле тяжести. [35]

В случае нежесткого симметричного волчка необходимо, кроме того, вводить поправку на центробежное искажение, особенно для высших вращательных уровней. Наконец, так же, как в случае линейных молекул, точность определения молекулярных параметров лимитируется наличием нулевой энергии. [36]

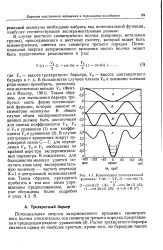Компоненты потенциальной функции. У ( а 2У ( 1 - cosna / 2. [37]

В случае жесткого симметричного волчка ( например, метильная группа), присоединенного к жесткому скелету, который может быть асимметричным, имеется ось симметрии третьего порядка. [38]

Молекулы типа плоского симметричного волчка всегда относятся к сплюснутым волчкам. [39]

Даже для почти симметричного волчка, как и в случае изогнуто-линейных переходов, появление подполос с необычными значениями ЬК может быть вызвано поворотом осей, если расположение главных осей в нижнем состоянии определяется не только симметрией молекулы ( см. выше. [40]

Действительно, пусть симметричный волчок вращается вокруг собственной оси; если пренебречь трением в точке его касания с полом, то единственной действующей на него силой будет сила тяжести, приложенная в центре тяжести. Эта сила направлена в плоскости чертежа вниз, и чтобы выяснить направление скорости точки приложения силы, нужно разложить силу G на две составляющие: вдоль оси симметрии ( эта составляющая компенсируется реакцией опоры) и по перпендикуляру к этой оси. [41]

Диаграмма уровней энергии симметричного волчка такого типа для случая Л 1 приведена на рис. 4.2. Для сравнения приведен также спектр ротатора. Знак или - относится к значению четности тт. Уровни с заданными значениями j и тг, которые, согласно (4.55), должны быть вырожденными, нарисованы слегка разделенными. [42]

Рассмотрим теперь поведение симметричного волчка, на который не действует момент сил. [43]

Задача о вращении симметричного волчка, точка опоры которого находится на оси симметрии, допускает, как указывалось, точное решение. В математическом отношении оно довольно сложно. Решение задачи о свободном симметричном волчке, наоборот, весьма просто, Мы получим его по методу, который был только что развит для произвольного свободного волчка. [44]

Один конец оси симметричного волчка закреплен, а другой свободно скользит по легкому направляющему желобу, выполненному в форме окружности, лежащей в вертикальной плоскости с центром в точке, где находится закрепленный конец оси; эта - окружность может вращаться вокруг вертикального диаметра, который неподвижен. [45]

Страницы: 1 2 3 4