Вычисление - кратный интеграл
Cтраница 2
В данном параграфе рассмотрим методы вычисления одномерных интегралов, а методы вычисления кратных интегралов будут изложены в главе 6 на примере задач нахождения угловых коэффициентов излучения. [16]
Тем самым все ранее изученные методы неопределенного интегрирования ставятся на службу вычислению кратных интегралов. [17]
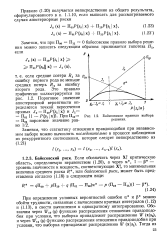 |
Байесовское правило выбора решения. [18] |
При определении условных вероятностей ошибок а и 5 можно обойти трудности, связанные с вычислением кратных интегралов (1.12) и (1.13), и свести вычисления к однократному интегрированию. [19]
Так как основные принципы построения программ вычисления дно - и многократных интегралов примерно одинаковые, будет приведена одна процедура вычисления кратных интегралов. [20]
Из математических задач, для которых разработано применение метода Монте-Карло, отметим следующие: решение систем линейных уравнений, обращение матриц, нахождение собственных значений и собственных векторов матрицы, вычисление кратных интегралов, решение задачи Дирихле, решение функциональных уравнений различных типов и др. Метод Монте-Карло успешно используется также для решения задач ядерной физики. Заметим, что для решения одной и той же конкретной задачи схема применения метода может быть существенно различной. [21]
Данная теорема утверждает равенство этих трех интегралов. Тем самым вычисление кратного интеграла сводится к вычислению одномерных интегралов по каждой переменной х, у в отдельности. [22]
Вычисление кратного интеграла связано с интегрированием функции нескольких переменных, заданной в некоторой области, ограниченной в общем случае криволинейными поверхностями. Существует большое число методов вычисления кратных интегралов, которые обычно аналогичны методам вычисления однократных интегралов. Так же как и для однократного интеграла, кратный интеграл заменяется линейной комбинацией значений интегрируемой функции в конечном числе точек. Отличие заключается в том, что область интегрирования является совокупностью точек n - мерного пространства, где п - кратность интеграла. [23]
Вычисление кратного интеграла связано с интегрированием функции нескольких переменных, заданной в некоторой области, ограниченной в общем случае криволинейными поверхностями. Существует большое число методов вычисления кратных интегралов, которые обычно аналогичны методам вычисления однократных интегралов. Так же как и для однократного интеграла, кратный интеграл заменяется линейной комбинацией значений интегрируемой функции в конечном числе точек. Отличие заключается в том, что область интегрирования является совокупностью точек тг-мерного пространства, где п - кратность интеграла. [24]
Кроме того, на практике подынтегральная функция f ( х) часто задается таблично и тогда само понятие первообразной теряет смысл. Аналогичные вопросы возникают при вычислении кратных интегралов. Поэтому важное значение имеют приближенные и в первую очередь численные методы вычисления определенных интегралов. [25]
 |
Интегрирование по Ньютону - Котесу дри п - 6. [26] |
Однако во многих случаях первообразная: функция F ( x) не может быть определена или же функция f ( x) задана в узлах некоторой сетки. Аналогичные вопросы возникают и при вычислении кратных интегралов. [27]
Использование этих свойств часто существенно облегчает вычисление конкретных кратных интегралов. [28]
По реализации гт удобно получать числовые значения моментов тт. Их вычисление по формулам работы [3] также связно с вычислением кратных интегралов от плотностей нормального распределения. [29]
Для ряда классов задач, где эти интегралы не вычисляются в явном виде, может оказаться разумным найти эти интегралы при помощи численного интегрирования. Эта дополнительная работа оправдывается, если получившиеся формулы используются многократно, например, при вычислении большой серии интегралов, при вычислении кратных интегралов как повторных ( см. гл. [30]
Страницы: 1 2 3