Безрисковый актив

Cтраница 2

Рассматривается однопериодный рынок, на котором обращаются безрисковый актив, рисковый актив ( акции) и опционы колл и пут на этот актив. Иногда под однопериодным рынком имеют в виду рынок, на котором исполнение опционов однократно на рассматриваемом интервале времени, но при этом динамика цен активов и процесс принятия решений о переформировании портфелей непрерывны. Мы же здесь под однопериодным рынком понимаем совсем простую временную конструкцию, охватывающую всего лишь два момента времени - начало и конец периода. Именно на ней мы попытаемся прояснить особенности взаимоотношений инвестора и рынка. [16]

Прежде считалось, что доля, инвестированная в безрисковый актив и обозначавшаяся через Х4, является положительным числом от нуля до единицы. Поскольку теперь имеется возможность получать заем по той же процентной ставке, то эти ограничения с Х4 снимаются. [17]

Прежде считалось, что доля, инвестированная в безрисковый актив и обозначавшаяся через ЛГ4, является положительным числом от нуля до единицы. Поскольку теперь имеется возможность получать заем по той же процентной ставке, то эти ограничения с Х4 снимаются. [18]

Любой портфель, состоящий из инвестиций в РАС и в безрисковый актив, имеет ожидаемый доход и стандартное отклонение, которые могут быть подсчитаны аналогично тому, как это было сделано для комбинаций некоторого актива и безрискового актива. [19]

На рис. 9.2 показано, что портфель лежит на прямой линии, соединяющей безрисковый актив и РАС. Конкретный портфель обозначен точкой Р на этой прямой. Другие портфели, состоящие из различных комбинаций РАС и безрискового актива, также будут располагаться на этой линии. Точное их расположение будет зависеть от относительных пропорций инвестиций в РАС и безрисковый актив. Например, портфель, состоящий из инвестиций в пропорции 0 50 в РАС и 0 50 в безрисковый актив, будет расположен точно посередине между двумя концами. [20]

Синтетический опцион можно создать с помощью инвестирования соответствующих сумм в базисный актив и безрисковый актив. С изменением цены базисного актива должно меняться и распределение средств между активами. [21]

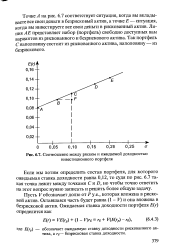Соотношение между риском и ожидаемой доходностью инвестиционного портфеля. [24]

Точке А на рис. 6.7 соответствует ситуация, когда вы вкладываете все свои деньги в безрисковый актив, а точке Е - ситуация, когда вы инвестируете все свои деньги в рискованный актив. Линия АЕ представляет набор ( портфель) свободно доступных вам вариантов из рискованного и безрискового актива. Так портфель С наполовину состоит из рискованного актива, наполовину - из безрискового. [25]

При анализе сначала определяется ожидаемая доходность и стандартное отклонение для портфеля, состоящего из инвестиции в безрисковый актив в сочетании с одной рискованной ценной бумагой. [26]

Если инвестор абсолютно не склонен к риску, то оптимальный портфель будет состоять из инвестиции только в безрисковый актив. Заимствования могут рассматриваться как предоставленная инвестору возможность приобретать ценные бумаги за счет кредита брокера по желанию инвестора. [27]

Докажите, что сильно нерасположенный к риску инвестор в оптимуме вложит более высокую долю своего портфеля в безрисковый актив, чем слабо нерасположенный к риску. [28]

Оптимальное сочетание рискованных активов обнаруживается в общей точке пересечения прямой, которая начинается в точке, представляющей безрисковый актив ( на вертикальной оси), и границы эффективности рискованных активов. Отрезок, соединяющий точку безрискового актива и тангенциальную точку, которая соответствует оптимальной комбинации рискованных активов, представляет самые лучшие соотношения риск - доходность. [29]

Если инвестор абсолютно не склонен к риску, то оптимальный портфель будет состоять из инвестиции только в безрисковый актив. [30]

Страницы: 1 2 3 4