Дифференцирование - интеграл
Cтраница 3
Дифференцируя ( 20) последовательно m раз и используя формулу дифференцирования интеграла по параметру ( см. стр. [31]
Остается еще предпоследний член в (5.2), который получился при дифференцировании интеграла по времени по верхнему пределу. [32]
Если точка у лежит на положительном расстоянии от области V, то дифференцирование интеграла ( 6) по координатам точки у можно произвести под знаком интеграла ( 3.35 г), так как вместе с функцией 1 / к-у п - 1 он имеет производные любого порядка. [33]
Заметим, что к понятию сингулярного интеграла приходят, в частности, при рассмотрении вопроса о дифференцировании интегралов, зависящих от параметра. Известно, что производная интеграла по параметру совпадает с интегралом от производной по параметру подынтегрального выражения, если последний равномерно сходится по этому параметру. [34]
При ее вычислении нужно принимать во внимание определение переменной xm i согласно уравнению ( IV, 194), что приводит к необходимости дифференцирования интегралов в выражении ( IV212) по верхнему пределу интегрирования. [35]
Действительно, для первого слагаемого справа стремление к нулю следует из второй теоремы Римана [ в силу леммы п 748 ], а по теореме о дифференцировании интеграла по переменному верхнему пределу [305, 12 ] то же заключение оказывается справедливым и для суммы двух других слагаемых. [36]
То, что дифференцирование и интегрирование - взаимно обратные операции, можно показать двумя способами, и от школьников следует потребовать понимания обоих способов, ибо оба доказательства парадигматичны для многочисленных приложений дифференциального отношения и интеграла. Во-первых, следует показать, что дифференцирование интеграла с переменным верхним пределом приводит к исходной функции, и во-вторых, что интегрирование дифференциального отношения воспроизводит исходную функцию с точностью до постоянного слагаемого. [37]
Последнее равенство показывает, что для Л 0 свертки по ( t x) функции С с ограниченными функциями ограничены. Из первого соотношения в (8.4.2) и правил дифференцирования интегралов получаем следующий результат. [38]
Вторая глава посвящена определенному интегралу. Рассматриваются определение и свойства интеграла Римана, формула Ньютона-Лейбница, правило дифференцирования интеграла с переменными верхним и нижним пределами интегрирования, формулы замены переменного и интегрирования по частям, различные методы оценки и приближенного вычисления интегралов. Много внимания уделяется приложениям определенного интеграла к решению геометрических и физических задач. [39]
К вычислению производной (1.54) можно подходить двояко. Один способ состоит в использовании физического закона сохранения массы, а другой - в применении правила дифференцирования интеграла с переменной областью интегрирования. Вычислим производную (1.54) каждым из этих методов и сравним результаты вычисления. [40]
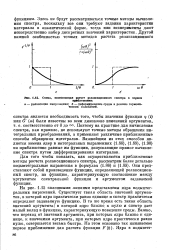 |
Схема, поясняющая расчет релаксационного спектра в первом. [41] |
Поэтому на практике для вычисления спектра, как правило, не используют точные методы обращения интегральных преобразований, а применяют различные приближенные способы обращения интегралов. Важнейшим из этих способов является замена ядер в интегральных выражениях (1.86), (1.89), (1.90) на приближенно равные им функции, допускающие прямое вычисление спектра путем дифференцирования интегралов. [42]
Дифференцируя его по т и предполагая, что р зависит только от переменной интегрирования т, но не зависит от мгновенного значения ти, получим искомую величину по правилу дифференцирования интеграла с переменным верхним пределом. [43]
Страницы: 1 2 3