Аргумент - косинус
Cтраница 1
Аргумент косинуса составляет сумма со / а. [1]
Аргумент косинуса составляет сумма ( ut а. [2]
Аргумент косинуса в (1.22) называется фазой волны. [3]
Аргумент косинуса составляет сумма wt - - a. [4]
Аргумент косинуса ( в данном случае of) называется фазой. [5]
Если к аргументам косинуса или синуса прибавить я нечетное число раз, знаки этих функций изменятся на обратные. [6]
В уравнении плоской волны аргумент косинуса содержит скалярное произведение векторов k и г. В уравнении сферической волны - произведение волнового числа k на расстояние г точки наблюдения от источника волны. [7]
Член 2тг ьоте в аргументе косинуса приводит к синусоидальным осцилляциям при движении источника по интерференционной диаграмме. [8]
Волновой процесс - это процесс двоякопериодический: аргумент косинуса в формуле ( 4) зависит от двух переменных - времени t и координаты у. Таким образом, волна имеет двойную периодичность - в пространстве и во времени. Для данного момента времени t уравнение ( 4) дает распределение смещения частиц х как функцию их расстояния у от начала координат; частицы, колеблющиеся под влиянием бегущей волны в данный момент времени t расположены по косинусоиде. [9]
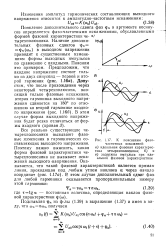 |
К пояснению фазо. [10] |
Появление дополнительного сдвига фаз г зп в аргументе косинусов определяется фазо-частотными искажениями, обусловленными формой фазовой характеристики че-тырехполюсника. Наличие дополни-тельных фазовых сдвигов ifn tj n ( con) в выходном напряжении приводит к существенным изменениям формы выходных импульсов по сравнению с входными. [11]
В дальнейшем воспользуемся тем обстоятельством, что добавка ф0 в аргумент косинуса не меняет характера движения, а означает лишь изменение начального момента в отсчете времени. [12]
Формулы (5.12) и (5.15) отличаются друг от друга только знаком аргумента косинуса в числителе. Поскольку косинус - функция четная, то это различие не может оказать влияние на последующие выкладки. [13]
Для того чтобы амплитуда этой стоячей волны обратилась в нуль, необходимо, чтобы аргумент косинуса стал равным гатг тг / 2, а аргумент синуса га тг, где т и га / - целые числа. Узловые поверхности гауссова пучка совместим с поверхностью зеркала в два приема. [14]
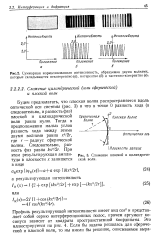 |
Сложение плоской и цилиндрической волн. [15] |
Страницы: 1 2 3