Асимптотик

Cтраница 2

Все асимптотики сопрягаются только частично. Невозможно сделать что-либо больше, чтобы сблизить их в глубине тела: число свободных параметров недостаточно. [16]

Сопоставим асимптотики (2.18) и (2.21), полученные для больших времен и расстояний, то есть вдали от источника. [17]

Определим асимптотики выражения ( 13) для больших значений времени и расстояния. [18]

Данные уточненные асимптотики решений установил Я. [19]

Рассматривая асимптотики функции Эй-ри, мы обнаружили, что функция Эйри меняет свое поведение в зависимости от знака аргумента: при отрицательных значениях аргумента она осциллирует, а в области положительных значений - экспоненциально убывает. Осцилляции появляются в результате интерференции вкладов от двух точек, в которых комплексные фазы стационарны и различны, в то время как затухающее поведение обусловлено вкладом одной точки стационарной фазы с действительным показателем экспоненты. [20]

Учитывая асимптотику (4.75) и R a b R %, заключаем, что система (4.89) принадлежит к типу нормальных систем Пуанкаре-Коха. [21]

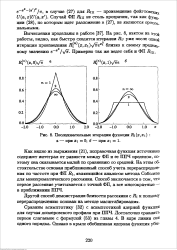Последовательные итерации функции RI ( XXI. а - при a. i 0. б - при х 1. [22]

Сравним асимптотику ( 32) с асимптотикой ядерной функций для случая доплеровского профиля при ППЧ. [23]

Найти асимптотику нулей функции Д () указанного вида уже возможно. Асимптотические формулы для корней таких функций Д ( А) находятся, например, методом последовательных приближений. Соответствующие формулы будут приведены в следующей главе. [24]

Причем асимптотику волновой функции в каналах, отличающихся группировкой частиц, удобно записывать с помощью разных систем координат Якоби. [25]

Зная асимптотику функции JE ( а, а), перейдем теперь к определению Гт, когда т не велико. [26]

Вычислим асимптотику корней уравнения ( 15) при Я - оо, Допустим, что уравнение ( 15) имеет при всех достаточно больших Я, корень z z ( K); тогда z ( K) - oo при Я - - оо. [27]

Что касается асимптотики, то авторы интересуются случаем, когда л не мало, а, напротив, велико. Такое уравнение тоже принадлежит к типу сингулярно возмущенных, но описывает колебания, не близкие к гармоническим, как в случае (7.96), а колебания иного типа - так называемые релаксационные колебания. Розова посвящена асимптотической теории релаксационных колебаний для систем общего вида, развитой Л. С. Понтрягиным и авторами монографии. [28]

Если соединить асимптотики (6.3) и (6.4) плавными линиями без экстремумов, то получатся кривые, представленные на рис. 6.1. Если точка на кривой расположена в верхней полуплоскости j3 0, то кондактанс у растет с ростом L, В нижней полуплоскости / 3 0 кондактанс у уменьшается с ростом L. [29]

Характер этой асимптотики можно выявить при помощи асимптотического анализа ( см., например, [5]), выделяя в исходцых уравнениях малый параметр, равный отношению характерных времен химической реакции и диффузии. [30]

Страницы: 1 2 3 4