Матрица - перенос
Cтраница 1
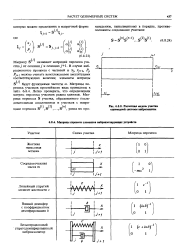 |
Расчетная модель участка одномерной системы внброзшцнты. [1] |
Матрицы переноса участков простейшего вида приведены в табл. 6.8.4. Легко проверить, что определители матриц переноса участков равны единице. [2]
Матрица переноса в (4.92) содержит нулевой элемент. [3]
Матрица переноса Гс по сравнению с (3.102) не претерпевает в данном случае никаких изменений. В табл. 11 приведены матрицы переноса для ряда типовых соединений элементов. [4]
Матрица переноса совокупности последовательно соединенных участков. [5]
Матрица переноса совокупности параллельно соединенных участков. [6]
Матрица переноса совокупности последовательно соединенных участков. [7]
Матрица переноса совокупности параллельно соединенных участков. [8]
Матрица переноса толстой линзы может быть разложена и другим способом: на простые матрицы, соответствующие двум тонким линзам и дрейфовому интервалу d между ними. [9]
Метод матрицы переноса, обсужденный в предыдущем разделе, может быть развит для рассмотрения самоподобных структур, скажем для блужданий на двумерной решетке. Ключевым моментом в этом подходе является то, что, во-первых, матрицы переноса можно применять не только на прямых лентах, но и на изогнутых, даже с большим числом изгибов. Такое блуждание без самопересечений следующего, более высокого уровня может быть теперь уложено на ленте в w раз шире с помощью аналогичных методов матрицы переноса, и весь процесс перенормировки повторяется. [10]
След матрицы переноса содержит полную информацию о том, является данное состояние локализованным или нет. [11]
Теория матриц переноса, на основе которой получены рассмотренные выше результаты, оказалась плодотворной во многих отношениях. В своей основополагающей работе Уно и Матида 82 с помощью этой теории установили ряд принципиальных закономерностей, которые мы детально рассмотрим. [12]
Сравнение матриц переноса в (4.130) и в (4.133) приводит к (4.112), которое означает, что фокусные расстояния каждой из двух тонких линз должны быть равны соответствующим фокусным расстояниям комбинированной толстой линзы, эквивалентной системе двух тонких линз. [13]
 |
Телескопическая система двух линз. [14] |
Используем матрицу переноса (4.133) и приравняем mz к нулю. [15]
Страницы: 1 2 3 4