Матрица - перенос
Cтраница 3
Следовательно, в статистической механике термодинамические свойства системы определяются наибольшим собственным значением матрицы переноса. [31]
Для каждого из механизмов, представляющего собой цепную систему, может быть записана матрица переноса Г -, полученная перемножением в обратном порядке матриц переноса входящих в него простых элементов. [32]
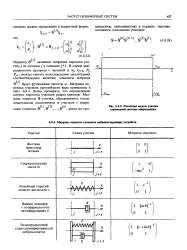 |
Расчетная модель участка одномерной системы внброзшцнты. [33] |
Матрицы переноса участков простейшего вида приведены в табл. 6.8.4. Легко проверить, что определители матриц переноса участков равны единице. [34]
В этой главе мы выведем гамильтониан Когута - Саскинда из теории Вильсона, используя метод матрицы переноса, аналогично тому, как это сделано в гл. Рассматриваемый ниже способ вывода позволяет наглядно продемонстрировать эквивалентность этих двух подходов. Выбор одного из них зависит от вкуса и от конкретного рассматриваемого вопроса. В вильсоновской теории симметрия между пространством и временем заложена в явном виде, спектр частиц определяется структурой особенностей функций Грина и налицо простая аналогия со статистической механикой. В подходе Когута - Саскинда мы имеем дело с привычной квантовомеханической системой и гамильтонианом, спектр частиц непосредственно определяется спектром самого гамильтониана, а фазовые переходы связаны с пересечением уровней энергии в пределе бесконечного объема. [35]
Соответствующим выбором этих параметров матрица в (4.130) может быть превращена в любую матрицу размерами 2x2, например в матрицу переноса толстой линзы. Это означает, что любая толстая линза может быть заменена на совокупность тонкой линзы и двух дрейфовых интервалов. Докажем, что эта замена эквивалентна введению главных плоскостей. [36]
Таким образом, для замкнутой цепочки задача нахождения функции распределения сводится к определению суммы диагональных элементов ( или шпура) матрицы переноса Л - степени. Далее, шпур матрицы - просто сумма ее собственных значений. [37]
Теперь рассмотрим решение задачи об определении спектра собственных частот для динамической модели, показанной на рис. 72, по методу матриц переноса. [38]
Для каждого из механизмов, представляющего собой цепную систему, может быть записана матрица переноса Г -, полученная перемножением в обратном порядке матриц переноса входящих в него простых элементов. [39]
Если с обеих сторон тонкой линзы расположены два дрейфовых интервала: слева - длиной 1 и справа - длиной / 2, можно представить матрицу переноса системы в виде произведения трех матриц: tridiittz, m m и тй ап, где mdrim и mdriftz - матрицы переноса слева и справа от линзы соответственно, а miens - матрица переноса линзы. [40]
Структурная схема содержит блок управления БУ, блок сложения и вычитания БСВ, блок умножения и деления БПД, блок матриц сложения ВМС, блок матриц переносов БМП, блок индикации БИ. [41]
Если с обеих сторон тонкой линзы расположены два дрейфовых интервала: слева - длиной 1 и справа - длиной / 2, можно представить матрицу переноса системы в виде произведения трех матриц: tridiittz, m m и тй ап, где mdrim и mdriftz - матрицы переноса слева и справа от линзы соответственно, а miens - матрица переноса линзы. [42]
Если с обеих сторон тонкой линзы расположены два дрейфовых интервала: слева - длиной 1 и справа - длиной / 2, можно представить матрицу переноса системы в виде произведения трех матриц: tridiittz, m m и тй ап, где mdrim и mdriftz - матрицы переноса слева и справа от линзы соответственно, а miens - матрица переноса линзы. [43]
Рассмотрим этот процесс на примере блобов. Матрицы переноса для каждого блоба построены при осуществлении блуждания от одного края блоба до другого. Такие матрицы переноса перемножаются совместно всеми возможными способами для следующего блоба большего размера, и таким образом для него строится матрица переноса. Такое ограничение сводится к выбору особого матричного элемента различных произведений матриц переноса для блобов более низкого уровня, принимая равным ему матричный элемент матрицы переноса для следующего по размеру блоба. В результате итерационного процесса могут быть получены характеристики самоподобных подклассов всех блужданий без самопересечений. [44]
Для получения матрицы переноса всей кинематической цепи Г следует в обратном порядке перемножить матрицы Г / всех выделенных участков. [45]
Страницы: 1 2 3 4