Матрица - перенос
Cтраница 2
Далее вычисляется матрица переноса участка обода ] В между сечениями Х & и ХА Ь Поскольку система ураанений изгиба участка обода интегрируется, элементы матрицы В легко формируются. [16]
Такой метод матрицы переноса может применяться несколькими путями к целому ряду теоретико-графовых задач укладки. [17]
В табл. 5 приведены матрицы переноса простейших элементов, из которых обычно мпонуются расчетные модели виброзащигных систем, трактуемых как системы сосредоточенными параметрами. [18]
Таким образом, разложение матрицы переноса толстой линзы на три более простые матрицы приводит к весьма наглядному представлению: фокусные расстояния тонкой линзы равны фокусным расстояниям толстой линзы, а два дрейфовых интервала определяют положение произвольных точек в пространстве объектов и изображений по отношению к соответствующим главным плоскостям толстой линзы. Толстая линза заменяется тремя простыми элементами, но при этом изменение координаты луча r ( z) внутри линзы учитывается соответствующим выбором дрейфовых интервалов. [19]
Вообще говоря, каждый элемент матрицы переноса (4.91) может иметь нулевое значение. Присутствие нулевого элемента означает, что некоторая характеристика выходящего луча не зависит от какой-то характеристики входящего пучка. [20]
После определения собственных частот с помощью матриц переноса легко найти формы колебаний. Для этого достаточно, приняв в одном сечении амплитуду за единицу и используя граничные условия, найти в других сечениях амплитуды, соответствующие рассматриваемой собственной частоте kr Полученные при этом значения являются коэффициентами формы. Знак минус в коэффициенте формы указывает на то, что колебания в рассматриваемом сечении и в сечении, где коэффициент формы принят равным единице, находятся в противофазе. [21]
Как уже отмечалось выше, метод матриц переноса все еще можно применять приближенно, представляя медленно меняющийся потенциал в виде нескольких постоянных ступенек потенциала. При этих энергиях электрона происходит резонансное туннелирование. В случае отличного от нуля смещения коэффициент пропускания не равен единице даже в условиях резонансного туннели-рования. [23]
В справедливости этого можно убедиться, используя аппарат матрицы переноса вдоль направления разделения г. С физической точки зрения это уравнение представляет собой юкавский обмен легчайшей частицей в данной теории. В случае нулевой массовой щели мы получаем степенной закон убывания сил, подобно тому как это имеет место в электродинамике. Заметим, что массовая щель не является локальным параметром порядка, поскольку ее определение содержит корреляции между асимптотически разделенными операторами. [24]
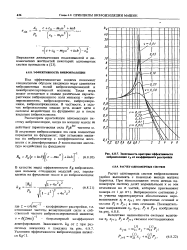 |
Зависимость критерия эффективности ввброизоляпвв kg от коэффициента расстройки. [25] |
Расчет одномерных систем виброизоляции удобно выполнять с помощью метода матриц Переноса. Вибрационное состояние j - го участка характеризуется абсолютными перемещениями Xj и Xj i ею граничных сечений и силами PJ и PJ I в этих сечениях. [26]
В силу П / f const преобразуемые с помощью матриц переноса амплитуды перемещений и сил являются функциями времени. Соответственно переменными оказываются собственные частоты рг и отношения между функциями Bjt отвечающими фиксированной частоте pr ( t), которые характеризуют форму колебаний. [27]
Тогда подставим Zi / Y и z2 F2 и напишем матрицу переноса в виде произведения трех матриц. Первая из них - матрица переноса второй тонкой линзы, окруженной двумя дрейфовцми интервалами li fi и lzh ( так как. [28]
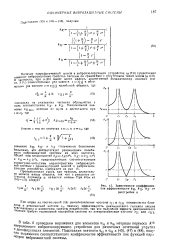 |
S. Зависимости коэффициентов эффективности / j, A, ft / от расстройки г. [29] |
В табл, 6 приведены выражения для элементов 12 и а22 матрицы переноса А 1 инерционного виброизолирующего устройства для различных сочетаний упругих и Демпфирующих элементов. [30]
Страницы: 1 2 3 4