Матрица - переходная вероятность
Cтраница 3
 |
Модель системы с очередью. [31] |
В дальнейшем, как и ранее, будем изучать однородные цепи Маркова, матрица переходных вероятностей которых не зависит от текущего времени. [32]
Маркова, и эти цепи независимы, однако имеют, вообще говоря, разные матрицы переходных вероятностей. [33]
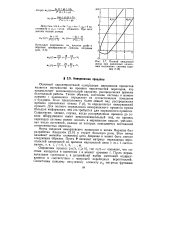 |
Полный ожидаемый доход при различных начальных состояниях системы ( пример. [34] |
Пусть первоначальное состояние I, а дальнейший выбор состояний осуществляется в соответствии с матрицей переходных вероятностей. [35]
Остальные характеристики остаются такими же, как и у модели Гилберта, так как матрица переходных вероятностей Р ( S) для этих моделей одинакова. [36]
Предполагается, что два состояния соответствуют требованиям налаженного процесса, для всех четырех состояний известна матрица переходных вероятностей. Марковский процесс, описывающий эту модель и класс решающих правил, приводит к предельному распределению и интегральному уравнению, посредством которых получаются оптимальные процедуры. [37]
Обратно, если для матрицы Q выполнены условия ( 95), то формула ( 94) определяет стандартную матрицу переходных вероятностей. [38]
Таким образом, для каждой однородной цепи Маркова матрица переходных вероятностей является стохастической и, наоборот, любую стохастическую матрицу можно рассматривать как матрицу переходных вероятностей некоторой однородной цепи Маркова. [39]
Уравнение (8.1) описывает процесс, свойства которого изменяются в случайные моменты времени, управляемые марковской цепью в, причем статистика переключений, определяемая матрицей переходных вероятностей этой цепи, предполагается не известной. [40]
Например, А имеет строки ( 1 / 3, 2 / 3) и ( 2 / 3, 1 / 3); это матрица переходных вероятностей, соответствующая цепи, образованной двумя состояниями Ei и Ez. [41]
В работе исследуются условия, при которых сумма независимых марковских последовательностей на конечной группе G также является простой однородной цепью Маркова на группе G с некоторой матрицей переходных вероятностей. Основные результаты получены для абелевых групп. Получено также полное описание устойчивых цепей. Доказательства используют новый подход, основанный на сведении задачи к выполнению соотношений определенного вида между характеристическими функциями строк соответствующих матриц переходных вероятностей. [42]
Поскольку рассмотрение двух крайних случаев сополиконденсации ( необратимой и равновесной) приводит к одному и тому же случайному процессу условного движения по цепи сополимера, можно заключить, что произвольная сополиконденсация мономеров с независимыми функциональными группами также описывается цепью Маркова с той же матрицей переходных вероятностей. Однако зависимость концентрации связей Q /, а следовательно, и LIJ от времени в общем случае должна быть определена из решения соответствующих кинетических уравнений с учетом обратимости элементарных реакций. [43]
Это число игр можно еще сократить, учитывая следующее: а) если первое действие одного из игроков дает ему больший выигрыш независимо от действия второго игрока, то второй игрок практически попадает в стационарную среду и в силу асимптотической оптимальности е-автоматов [ Цетлин и Гинзбург, 1968 ] при малых е выбирает действие 1; б) два соотношения вида 622 621 6ц &12 и 622 6ц 621 &12 заведомо дадут совпадающие матрицы переходных вероятностей ( это следует из тактики поведения е-автомата х)) и, следовательно, совпадающие результаты. [44]
Относительно матрицы переходных вероятностей jPrf состояние / возвратно и адариодично. [45]
Страницы: 1 2 3 4