Матрица - уравнение
Cтраница 3
Матрица податливости [ В ] является квазидиагональной матрицей, состоящей из блоков [ Bk для отдельных стержней. Матрицы уравнений равновесия и геометрических уравнений вследствие стати ко - геометрической аналогии являются взаимно транспонированными матрицами. [31]
Поэтому для сокращения времени решения системы уравнений ( IX, 20) можно применить метод сигнальных графов, который дает возможность получить аналитическое выражение связи входных и выходных параметров системы. Матрице уравнений связи ХТС ставится в соответствие сигнальный граф, который является ее топологическим представлением. Узлы графа отвечают переменным системы [ Xk, Yh ], а дуги характеризуют связь между ними, которая выражается коэффициентами матрицы уравнений связи. [32]
Характеристическое уравнение для уравнений неуправляемого бокового движения имеет один положительный, один отрицательный, один нулевой и два чисто мнимых корня. Преобразование матрицы уравнений неуправляемого бокового движения к диагональной форме позволяет оценить область управляемости для неустойчивого положения равновесия системы бокового движения и сформулировать требования к двигателю, прилагающему момент по оси кожуха маховика. [33]
Для опорных стержней в выражении (1.41) необходимо использовать только части, соответствующие узлу /, так как уравнения равновесия составляются только для узлов / - 4 фермы. Для ЭВМ такой способ построения матрицы уравнений равновесия является более удобным, чем последовательное вырезание узлов, которое используют при ручном счете. [34]
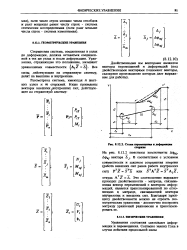 |
Схема перемещения м деформации стержня. [35] |
Это соотношение выражает принцип двойственности - матрица, связывающая вектор перемещений с вектором деформаций, является транспонированной по отношению к матрице, связывающей векторы внутренних и внешних сил. Благодаря принципу двойственности можно не строить геометрические уравнения - достаточно построить матрицу уравнений равновесия и транспонировать ее. [36]
Так как в настоящей работе; не рассмотрены случаи пластинки, содержащей более одного выреза, то матрица уравнений не выводилась и численные расчеты не проводились. В заключение можно отметить, что если размеры вырезов относительно большие и они расположены близко друг от друга, то, очевидно, матрица уравнений будет плохо обусловленной. [37]
Таким образом, переход от одного способа соединения станков в поточную линию к другому не требует введения новых n - матриц и изменения расположения n - матриц в уравнении. Отличие состоит только в том, что новые n - матрицы имеют компоненты, отличающиеся от компонент матриц прежнего уравнения и старая переменная заменяется новой переменной. [38]
Следовательно, только пять элементов вектора являются независимыми и вектор является пятимерным, а не шестимерным. Этот метод рассмотрения может быть обобщен и применен для последовательности любого числа адсорбированных веществ типа я, 1; любой столбец матрицы уравнения ( 353) в обобщенной форме может быть сведен к требуемой форме ( 354), если сумма его элементов равна нулю. Это всегда будет выполняться для всех адсорбированных веществ, которые не соответствуют свободным веществам. [39]
Пусть молекулярная система формально разделена на два фрагмента. Очевидно, что последовательный расчет фрагментов по схеме МО ЛКАО вместо одновременного расчета системы в целом возможен в том случае, если удается привести матрицу секу-лярного уравнения ( V. Тогда на ее диагонали расположатся две квадратные матрицы, так что ее детерминант станет равным произведению двух детерминантов меньшего порядка. В поисках условий, при которых это возможно, необходимо, в первую очередь. ПА, так как остальные атомы из разных фрагментов, как предполагается, пренебрежимо слабо взаимодействуют между собой из-за большого расстояния между ними. [40]
Таким образом, при интегрировании явным методом Эйлера уравнений состояния () с большими по модулю собственными значениями матриц коэффициентов шаг интегрирования по условиям устойчивости должен быть выбран достаточно малым. Такая ситуация возникает, например, при обработке уравнений электрических цепей с малыми постоянными времени, что соответствует большим по модулю вещественным частям собственных значений матриц уравнений состояния. При этом попытка увеличить шаг более величины, определяемой его максимальной оценкой, приводит к резкому возрастанию погрешности ( взрыву погрешности) и нарушению адекватности вычисленных значений истинному решению дифференциального уравнения. [41]
Как было показано в § 9.15, выбор шага, обеспечивающего заданный тип устойчивости решения, должен подчиняться определенным условиям, зависящим от собственных чисел матрицы уравнений состояния, или, что то же, от корней характеристического уравнения. [42]
Таким образом, при интегрировании явным методом Эйлера уравнений состояния (6.8) с большими по модулю собственными значениями матриц коэффициентов шаг интегрирования по условиям устойчивости должен быть выбран достаточно малым. Такая ситуация возникает, например, при обработке уравнений электрических цепей с малыми постоянными времени, что соответствует большим по модулю вещественным частям собственных значений матриц уравнений состояния. [43]
Как было показано в § 6.3, выбор шага, обеспечивающего заданный тип устойчивости решения, должен подчиняться определенным условиям, зависящим от собственных чисел матрицы уравнений состояния, или, что то же, от корней характеристического уравнения. [44]
Пользуясь ф-лами ( 19), ( 20), находим по коэф-там сопряженной матрицы уравнения линий влияния при нахождении груза в первом и втором пролетах. [45]
Страницы: 1 2 3 4