Порождающая матрица

Cтраница 2

Циклический код ( 7 4. Порождающий полином g p р3 р2 1. [16]

Как указано выше, порождающую матрицу для ( п, k) кода можно сконструировать из любого набора k линейно независимых кодовых слов. [17]

Таким образом, для любой порождающей матрицы G существует эквивалентная матрица G, которая, если не принимать во внимание расположение информационных символов, соответствует систематическому коду. Проверочная матрица Н для эквивалентного систематического кода имеет вид, аналогичный представленному на рис. 6.1.3, с той разницей, что единичная подматрица занимает те - ( N-L) строк, которые соответствуют положению проверочных символов, и эти строки не обязательно являются последними N-L строками. Синдром принятой последовательности у, как и прежде, определяется равенством S уЯ и можно, как и прежде, проводить декодирование на основе синдромной таблицы декодирования. [18]

Мы называем матрицу (7.8) стандартной формой порождающей матрицы G. Код С называется систематическим, если существует / г-подмно-жество координатных мест такое, что каждой возможной &-энке элементов на этих k местах соответствует ровно одно кодовое слово. Заметим, что согласно (7.8) всякий ( п, &) - код является систематическим. [19]

Рассмотрим любые d - 1 столбцов порождающей матрицы кода Л, и удалим их. [20]

Разрешенные кодовые комбинации кода с такой порождающей матрицей отличаются тем, что первые k символов в них совпадают с исходными информационными, а проверочными оказываются ( n - k) последних символов. [21]

Карлик [1969] показал, что такая форма порождающей матрицы двоичного КВ-кода очень полезна при исследовании весовой структуры кода. Так как порождающие матрицы многих хороших двоичных КВ-кодов могут быть представлены в виде (15.242), то Мак-Вильяме [1968, 1970] недавно предприняла попытку изучения новых кодов такого вида. Преимущество записи порождающей матрицы в форме, приведенной в теореме 15.24, показывает также доказательство следующей теоремы. [22]

Как и в случае вещественных решеток, определим порождающую матрицу М ( см. формулу ( 1) гл. [23]

Условия эргодичности СПКР легко выражаются в терминах характеристических чисел порождающей матрицы СПКР. [24]

ДЛЯ образуют симплициальный базис для АЛ и ДМ является порождающей матрицей для ДЛ. Хотя ДЛ зависит от того, какой используется симплициальный базис, ее детерминант остается неизменным. [25]

Очевидно, что строки G независимы и поэтому G есть порождающая матрица ( 11 6) - кода С над G. [26]

Рассмотрим код с проверкой на четность, у которого строки порождающей матрицы не являются линейно независимыми. Показать, что некоторая ненулевая информационная последовательность отображается в нулевое кодовое слово. Используя это, показать, что для каждой информационной последовательности существует по крайней мере одна другая информационная последовательность, которая отображается в то же самое кодовое слово. Ясно, что такие коды не интересны для практики. [27]

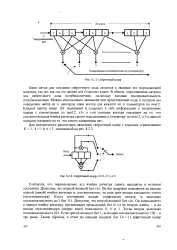Сверточный кодер.| Сверточный кодер с К3, kl, п3. [28]

Один метод для описания сверточного кода сводится к заданию его порождающей матрицы, так же, как мы это делали для блоковых кодов. В общем, порождающая матрица для сверточного кода полубесконечная, поскольку входная последовательность полубесконечная. [29]

Соответствующий 2-удлиненный код строится путем добавления единичного вектора длины N к порождающей матрице кода. Как видно из рис. 14.1, этот код получается из расширенного циклического кода с порождающим многочленом g ( x) l ( x 1) путем 1-удли-тгения с помощью общей проверки на четность. В большинстве случаев минимальный вес 2-удлиненного кода совпадает с минимальным весом исходного кода. Однако в некоторых случаях 2-удлинение кода приводит к уменьшению минимального расстояния. [30]

Страницы: 1 2 3 4